cho tam giác ABC, các đường cao BD và CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau tại K. Gọi M là trung điểm BC
a, CM: △ADB∼ΔAEC, ΔAED ∼ΔACB
b, CM: HE.HC=HD.HB
c, CM: H,M,K thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 7 2021
a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(cmt)
\(\widehat{A}\) chung
Do đó: ΔADE\(\sim\)ΔABC(c-g-c)
2 tháng 6 2023
c: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hbh
=>M là trung điểm của HK
=>H,M,K thẳng hàng
d: BACK là hình thoi
=>M là trung điểm của AK và AK vuông góc BC
=>A,H,M thẳng hàng
=>ΔABC cân tại A
=>AB=AC
T
3 tháng 6 2023
tham khảo
a.Ta có BK//CH(⊥AB),CK//BH(⊥AC)BK//CH(⊥AB),CK//BH(⊥AC)
→BHCK→BHCK là hình bình hành
b.Vì BHCKBHCK là hình bình hành
→HK∩BC→HK∩BC tại trung điểm mỗi đường
Do MM là trung điểm BCBC
→M→M là trung điểm HKHK
→H,M,K→H,M,K thẳng hàng
c.Ta có O,MO,M là trung điểm AK,HKAK,HK
→OM→OM là đường trung bình ΔAHKΔAHK
→OM//AH→OM//AH
Do BD∩CE=H→HBD∩CE=H→H là trực tâm ΔABC→AH⊥BCΔABC→AH⊥BC
→OM⊥BC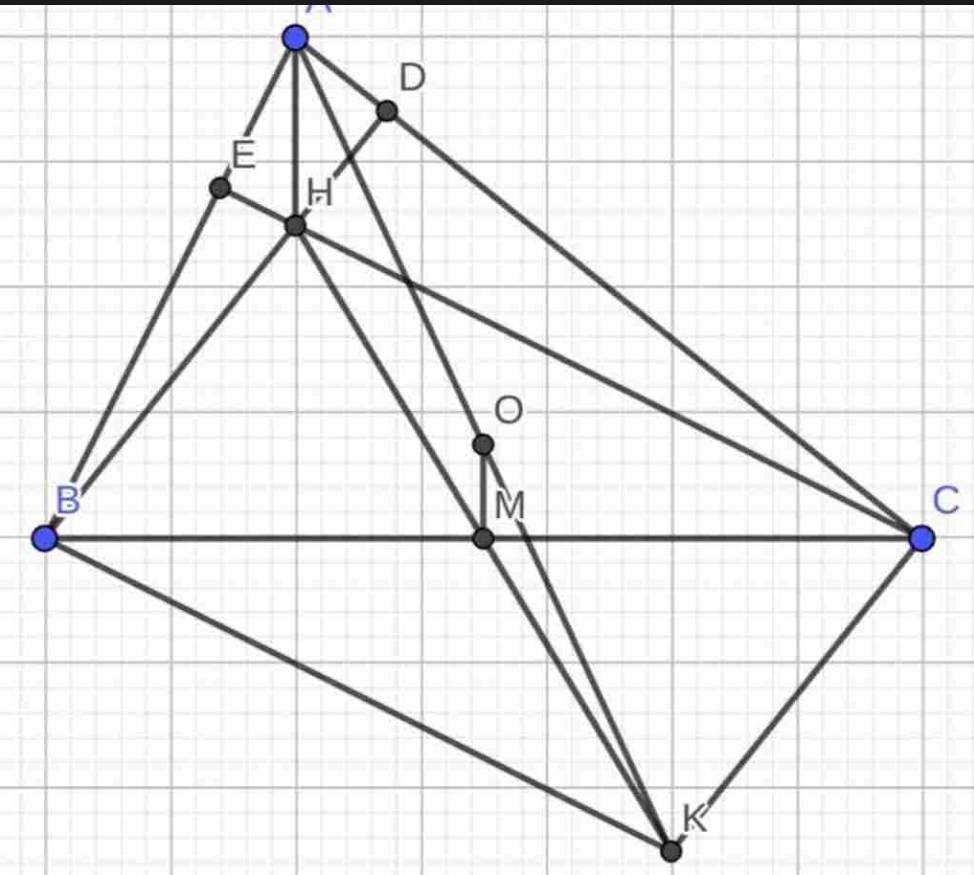
23 tháng 3 2021
a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
4 tháng 8 2021
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔABD\(\sim\)ΔACE(g-g)
b) Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)
Do đó: ΔHEB\(\sim\)ΔHDC(g-g)
Suy ra: \(\dfrac{HE}{HD}=\dfrac{HB}{HC}\)
hay \(HE\cdot HC=HB\cdot HD\)