Cho ΔABC nhọn (AB < AC). BD, CE là đường cao. Phân giác kẻ từ A của ΔABC cắt DE và BC lần lượt tại M, N. Giả sử \(AD=\frac{1}{2}AB\). Chứng minh : M là trung điểm của AN.
Giúp hộ !!! Thanks !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QP
16 tháng 8 2021
1)
Ta có : BD là đg trung tuyến của tam giác ABC (gt)
=> D là tđ của AC (1)
CE là đg trung tuyến của tam giác ABC (gt)
=>E là tđ của AB (2)
Từ (1),(2)
=>DE là đg trung bình của tam giác ABC
=>DE // BC : DE=1/2 BC
Thay BC=10cm
=>DE=5cm
2)
a) Ta có:MN // BC (gt)
=>MI // BC
Lại có:ED // BC (cmt)
=>MI // BC
Xét tam giác BED,có:
MI // BC
I là tđ của BD (gt)
=> MI là đg trung bình của tam giác BED
=>M là tđ của BE
b) Ta có: MN // BC (gt)
=>MK // BC
Xét tam giác BEC,có:
MK // BC (cmt)
M là tđ của BE (cmt)
=> MK là đg trung bình của tam giác BEC
c) ko đề
d) MK là đg trung bình của tam giác BEC (cmt)
=>MK=1/2 BC
=>MI + IK =1/2 BC
Thay MI =1/2 DE (MI là đg trung bình của tam giác BED)
=>1/2 DE + IK = 1/2 BC
=> IK =1/2 (BC-DE)
=>IK=1/2 DE (vì DE =1/2 BC)
Có: MI =1/2 DE (cmt)
KN =1/2 DE (cmt)
=>MI=KN=IK (=1/2 DE)
1 tháng 12 2023
a: Xét ΔOAD và ΔOMK có
\(\widehat{OAD}=\widehat{OMK}\)(hai góc so le trong, AD//MK)
\(\widehat{AOD}=\widehat{MOK}\)
Do đó: ΔOAD đồng dạng với ΔOMK
=>\(\dfrac{OA}{OM}=\dfrac{OD}{OK}\)
=>\(OA\cdot OK=OM\cdot OD\)
b: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{CA}\)
=>\(\dfrac{BD}{5}=\dfrac{CD}{10}\)
=>\(\dfrac{BD}{1}=\dfrac{CD}{2}\)
mà BD+CD=BC=12
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{1}=\dfrac{CD}{2}=\dfrac{BD+CD}{1+2}=\dfrac{12}{3}=4\)
=>\(BD=4\left(cm\right);CD=8\left(cm\right)\)
c: ME//AD
=>\(\widehat{AEK}=\widehat{DAC}\)(hai góc so le trong)(1)
KM//AD
=>\(\widehat{AKE}=\widehat{BAD}\)(hai góc đồng vị)(2)
AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{AEK}=\widehat{AKE}\)
=>AE=AK
Xét ΔCAD có EM//AD
nên \(\dfrac{CE}{CA}=\dfrac{CM}{CD}\)
=>\(\dfrac{CE}{CM}=\dfrac{CA}{CD}\)
mà \(\dfrac{CA}{CD}=\dfrac{BA}{BD}\)
nên \(\dfrac{CE}{CM}=\dfrac{BA}{BD}\)
=>\(\dfrac{AB}{BD}=\dfrac{EC}{CM}\)
=>\(\dfrac{AB}{EC}=\dfrac{BD}{CM}\)(ĐPCM)
22 tháng 2 2023
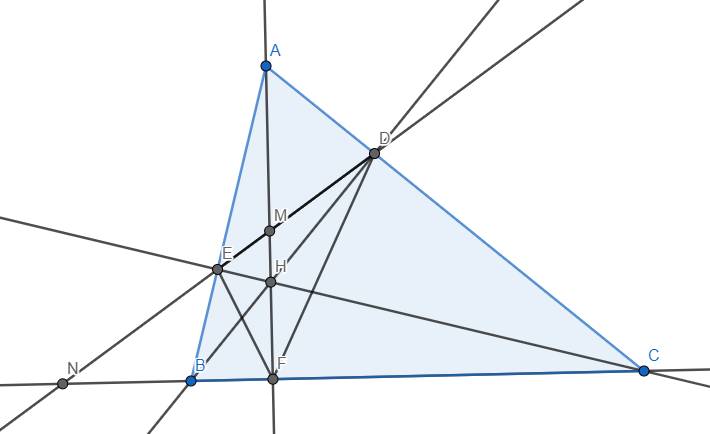
a) Xét \(\Delta ABD\) và \(\Delta ACE\), ta có \(\widehat{ADB}=\widehat{AEC}\left(=90^o\right)\) và góc A chung \(\Rightarrow\Delta ABD~\Delta ACE\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Rightarrowđpcm\)
b) Từ \(AE.AB=AD.AC\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét \(\Delta ADE\) và \(\Delta ABC\), ta có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) và góc A chung \(\Rightarrowđpcm\)
c) Do \(\Delta ADE~\Delta ABC\) \(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2\)
Lại có \(\dfrac{AD}{AB}=cosA=cos45^o=\dfrac{1}{\sqrt{2}}\) nên \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{1}{\sqrt{2}}\right)^2=\dfrac{1}{2}\)\(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}-S_{ADE}}=\dfrac{1}{2-1}\) \(\Rightarrow\dfrac{S_{ADE}}{S_{BEDC}}=1\)
d) Kẻ đường cao AF của tam giác ABC. Tương tự câu b, ta chứng minh được các tam giác BFE và CDF cùng đồng dạng với tam giác ABC. Từ đó suy ra \(\Delta BEF~\Delta DCF\) \(\Rightarrow\widehat{BFE}=\widehat{CFD}\) \(\Rightarrow90^o-\widehat{BFE}=90^o-\widehat{CFD}\) \(\Rightarrow\widehat{EFM}=\widehat{DFM}\) \(\Rightarrow\) FM là tia phân giác trong tam giác DEF \(\Rightarrow\dfrac{MD}{ME}=\dfrac{FD}{FE}\).
Mặt khác, \(FN\perp FM\) \(\Rightarrow\) FN là phân giác ngoài của tam giác DEF \(\Rightarrow\dfrac{ND}{NE}=\dfrac{FD}{FE}\). Từ đó suy ra \(\dfrac{MD}{ME}=\dfrac{ND}{NE}\) \(\Rightarrowđpcm\)
15 tháng 4 2023
góc BEC=1/2*180=90 độ
góc BDC=1/2*180=90 độ
Xét ΔABC có
BD,CE là đường cao
DB cắt CE tại H
=>H là trực tâm
=>AH vuông góc BC tại F
góc MDO=góc MDH+góc ODH
=góc MHD+góc DBC
=góc HBF+góc FHB=90 độ
=>DM là tiếp tuyến của (O)
6 tháng 3 2022
a, Xét tam giác ABD và tam giác ACE
^A _ chung
^ADB = ^AEC = 900
Vậy tam giác ABD ~ tam giác ACE (g.g)
b, Xét tam giác CBD và tam giác CAK ta có
^C _ chung
^CDB = ^CKA = 900
Vậy tam giác CDB ~ tam giác CKA (g.g)
\(\dfrac{CD}{CK}=\dfrac{CB}{CA}\Rightarrow CD.CA=CB.CK\)
c, Xét tam giác KDC và tam giác ABC
^C _ chung
\(\dfrac{DC}{BC}=\dfrac{KC}{AC}\)( tỉ lệ thức tỉ số đồng dạng )
Vậy tam giác KDC ~ tam giác ABC (c.g.c)
Xét \(\Delta ABD\)và \(\Delta ACE\)có:
\(\widehat{ADB}=\widehat{AEC}=90^o\); \(\widehat{BAC}\)( chung )
\(\Rightarrow\)\(\Delta ABD\approx\Delta ACE\left(g.g\right)\)
\(\Rightarrow\)\(\frac{AB}{AC}=\frac{AD}{AE}\)
Xét \(\Delta ADE\)và \(\Delta ABC\)có :
\(\frac{AB}{AC}=\frac{AD}{AE}\); \(\widehat{BAC}\)( chung )
\(\Rightarrow\Delta ADE\approx\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\widehat{D_1}=\widehat{ABC}\)
Xét \(\Delta ADM\)và \(\Delta ABN\)có :
\(\widehat{D_1}=\widehat{ABN}\); \(\widehat{A_1}=\widehat{A_2}\)
\(\Rightarrow\Delta ADM\approx\Delta ABN\left(g.g\right)\)
\(\Rightarrow\frac{AD}{AB}=\frac{AM}{AN}=\frac{1}{2}\)
Vậy M là trung điểm AN