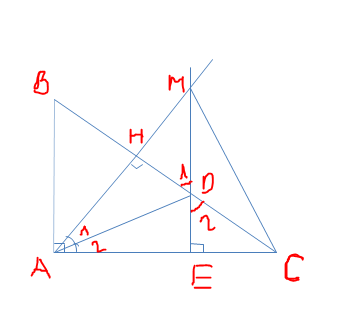
Cho tam giác ABC vuông tại A, đường cao AH. Phan giác góc ABC cắt AH tại D. Kẻ DM vuông góc với AB ( M thuộc AB ). Đường thẳng MD cắt BC tại N
1) Chứng minh tam giác BMD = tam giác BHD
2. Chứng minh tam giác ADN là tam giác cân và AN là tia phân giác của góc HAC
3. Cho BD = 2 (đơn vị độ dài). Chứng minh AB - AD > 1 (đơn vị độ dài)


a, xét tam giác BMD và tam giác BHD có : BD chung
góc ABD = góc DBH do BD là phân giác của góc ABC (gt)
góc DMB = góc DHB = 90
=> tam giác BMD = tam giác BHD (ch - gn)
b, xét tam giác ADM và tam giác NDH có : góc NDH = góc MDA (đối đỉnh)
góc NHD = góc DMA = 90
MD = DH do tam giác BMD = tam giác BHD (Câu a)
=> tam giác ADM = tam giác NDH (cgv-gnk)
=> DA = DN (đn)
=> tam giác ADN cân tại D (Đn)