Số phần tử của tập hợp các số thỏa mãn
là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 6 2016
abc + cba = 100a + 10b + c + 100c + 10b + a = 101a + 20b + 101c = 101(a + c) + 20b = 101.9 + 20b = 909 + 20b < 1000 (vì nó có 3 chữ số )
=> 20b < 1000 - 909 = 91 => b < \(\frac{91}{20}=4\frac{11}{20}\)
=> A = { b \(\in N\); b < \(4\frac{11}{20}\)} = { 0 ; 1 ; 2 ; 3 ; 4 } có 5 phần tử
6 tháng 4 2016
vì a+c =9 nên để tổng abc+cba là số có 3 chử số thì tổng hàng chục b+b <10 nên b<5. vậy tập hợp A có 5 giá trị là 0,1,2,3,4
16 tháng 7 2016
Theo đầu bài ta có:
abc + cba
= ( 100a + 10b + c ) + ( 100c + 10b + a )
= ( 100a + a ) + ( c + 100c ) + ( 10b + 10b )
= 101a + 101c + 20b
= 101 ( a + c ) + 20b
Do a + c = 9 nên:
= 101 * 9 + 20b
= 909 + 20b
- Do abc + cba là 1 số có 3 chữ số nên abc + cba < 1000 => 909 + 20b < 1000 => 20b < 91 => b < 4,55
- Do A là tập hợp các giá trị của chữ số b thỏa mãn điều kiện trên nên A = { 0 ; 1 ; 2 ; 3 ; 4 }
Vậy tập hợp A có 5 phần tử.
HL
4
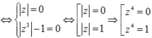
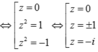
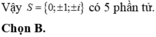
vì: lx ‐ 2,5l ≥ 0
và l3,5 ‐ xl ≥ 0
=> để lx ‐ 2,5l + l3,5 ‐ xl = 0
thì x ‐ 2,5 = 0 và 3,5 ‐ x = 0
=> x ‐ 2,5 = 3,5 ‐ x =>
x + x = 3,5 + 2,5 = 0 =>
x ∈ ϕ
Vậy...
|x - 2,5| + |3,5 - x| = 0
Mà |x - 2,5| \(\ge\) 0 ; |3,5 - x| \(\ge\) 0
Nên |x - 2,5| = |3,5 - x| = 0
|x - 2,5| = 0 => x - 2,5 = 0 => x = 2,5
|3,5 - x| = 0 => 3,5 - x = 0 => x = 3,5
Mà \(2,5\ne3,5\) nên số phần tử là 0