Cho tam giác ABC vuông tại A, O là giao điểm các đường p.giác. OA = \(\sqrt{2}\). Tính Khoảng cách từ O đến BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


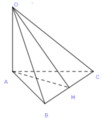
Gọi H là chân đường cao kẻ từ A xuống BC trong tam giác ABC.
+ Ta có: A H ⊥ B C O A ⊥ B C ⇒ B C ⊥ O A H ⇒ O H ⊥ B C ⇒ d(O; BC) = OH
+ Nửa chu vi tam giác ABC: p = 14 + 16 + 10 2 = 20
S A B C = 20 20 − 14 20 − 16 20 − 10 = 40 3 (theo công thức Hê-rông)
Lại có S A B C = 1/2AH.BC ⇒ AH = 2 S A B C B C = 80 3 10 = 8 3 .
+ Tam giác OAH vuông tại A (OA ⊥ AH)
⇒ OH = O A 2 + A H 2 = 8 2 + 8 3 2 = 16.
Vậy d(O; BC) = OH = 16.
Đáp án B

a) Tam giác ABC vuông tại A => AB2=BC2-AC2 => AB2=132-52 <=> AB2=169-25=144 => AC=12
b) Giao điểm của 3 đường trung trực trong tam giác cách đều 3 đỉnh của tam giác đó. Mà OA=OB=OC
=> O là giao điểm của 3 đường trung trực trong tam gaics ABC.
c) Tam giác ABC vuông tại A => Giao của 3 đường trung trực trong tam giác ABC nằm trên cạnh BC
Mà OB=OC => Trung điểm của BC trùng với điểm O => AO là trung tuyến của tam giác ABC.
G là trọng tâm => GO=1/3AO=1/3BO=1/3CO. BO=CO=1/2BC =>BO=CO=13/2=6,5 (cm)
=> GO=1/3.6,5\(\approx\)2,1 (cm)
Khoảng cách từ O đến BC cũng là khoảng cách từ O đến AB,AC.
Mà \(OA=\sqrt{2}\Rightarrow OA=OB=OC=\sqrt{2}\)
Hay khoảng cách từ OB đến BC là \(\sqrt{2}\)
O là giao 3 đường phân giác
=> O là tâm đường tròn nội tiếp của tam giác ABC
=> khoảng cách từ O đến BC = khoảng cách từ O đến AB
Kẻ OH vuông với AB tại H
=> khoảng cách từ O đến BC = khoảng cách từ O đến AB = OH
Xét tam giác AHO vuông tại H
\(\widehat{OAH}=\frac{\widehat{ABC}}{2}=\frac{90^o}{2}=45^o\)
=> Tam giác AHO vuông cân tại H
=> AH=HO
Áp dụng định lí Pitago ta có:
\(AO^2=AH^2+HO^2=2HO^2\Rightarrow2=2.HO^2\Rightarrow HO^2=1\Rightarrow OH=1\)
Vậy khoản cách từ O đến BC là 1