Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O.Biết SA⊥(ABCD), SA = \(\frac{a\sqrt{3}}{3}\)
a. Chứng minh BC⊥SBBC⊥SB
b. Gọi M là trung điểm của SC. Chứng minh (BDM)⊥(ABCD)(BDM)⊥(ABCD)
c. Tính góc giữa đường thẳng SB và mp(SAC).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 4 2023
1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>(SAB) vuông góc (SBC)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
\(AC=\sqrt{AB^2+BC^2}=2a\) \(\Rightarrow AO=\dfrac{1}{2}AC=a\) ; \(AM=\dfrac{1}{2}AO=\dfrac{a}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD) \(\Rightarrow\widehat{SCA}=45^0\)
\(\Rightarrow SA=AC.tan45^0=2a\)
\(AB^2=a^2\) ; \(AM.AC=\dfrac{a}{2}.2a=a^2\Rightarrow AB^2=AM.AC\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AC}{AB}\Rightarrow\Delta ABM\sim\Delta ACB\left(c.g.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{ABC}=90^0\Rightarrow BM\perp AC\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BM\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\left(SBM\right)\perp\left(SAC\right)\)
CM
19 tháng 4 2018
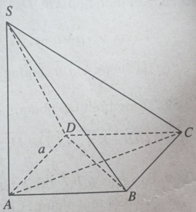
a) (BD ⊥ SA & BD ⊥ AC ⇒ BD ⊥ (SAC)
⇒ BC ⊥ SC.
b) (BC ⊥ SA & BC ⊥ AB ⇒ BC ⊥ (SAB)
⇒ (SBC) ⊥ (SAB).
c) + Xác định góc α giữa đường thẳng SC và mp(ABCD):
(C ∈(ABCD) & SA ⊥ (ABCD) ⇒ ∠[(SC,(ABCD))] = ∠(ACS) = α
+ Tính góc:
Tam tam giác vuông SCA, ta có:
tanα = SA/AC = √3/3 ⇒ α = 30 o .
17 tháng 11 2023
a: Xét ΔSAB có
M,N lần lượt là trung điểm của SA,SB
=>MN là đường trung bình cuả ΔSAB
=>MN//AB
MN//AB
AB\(\subset\)(ABCD)
MN không nằm trong mp(ABCD)
Do đó: MN//(ABCD)
b: Xét ΔSCB có
N,P lần lượt là trung điểm của SB,SC
=>NP là đường trung bình của ΔSBC
=>NP//BC
NP//BC
BC\(\subset\)(ABCD)
NP không nằm trong mp(ABCD)
Do đó: NP//(ABCD)
c: NP//(ABCD)
MN//(ABCD)
MN,NP nằm trong mp(MNP)
Do đó: (MNP)//(ABCD)
22 tháng 4 2023
1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
BD vuông góc CA
BD vuông góc SA
=>BD vuông góc (SAC)
2: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SCD) vuông góc (SAD)
4: (SC;(SAB))=(SC;SB)=góc CSB
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{AC^2+SA^2}=a\sqrt{5}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
BC=a
Vì SB^2+BC^2=SC^2
nên ΔSCB vuông tại B
sin CSB=BC/SC=1/căn 5
=>góc CSB=27 độ
23 tháng 10 2023
a: Xét ΔSAB có
M,N lần lượt là trung điểm của SA,SB
=>MN là đường trung bình
=>MN//AB
=>MN//(ABCD)
b; Xét ΔSBC có
N,P lần lượt là trung điểm của SB,SC
=>NP là đường trung bình
=>NP//BC
=>NP//(ABCD)
c: MN//(ABCD)
NP//(ABCD)
\(MN,NP\subset\left(MNP\right)\)
Do đó: (MNP)//(ABCD)