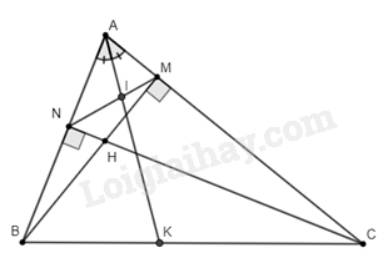
Cho tam giác BCD nhọn, các đường cao CE và DF cắt nhau tại I. Chứng Minh
a)\(\Delta BEC\omega\Delta DFB\)
b)\(\widehat{FEB}=\widehat{DCB}\)
c) Trên E lấy EC và DF lần lượt hai điểm P và Q sao cho \(\widehat{BPD}=\widehat{BQC}=90^o\). Chứng minh BP=BQ

mk bo tay
hoi chi GOOGLE nha ban
...
Xét \(\Delta BEC\)Và \(\Delta BFD\) có :
\(\widehat{BEC}\) \(=\)\(\widehat{BFD}\) ( cùng = 900 )
\(\widehat{B}\) chung
\(\Rightarrow\)\(\Delta BEC\) \(~\)\(\Delta BFD\) ( g - g )
Do \(\Delta BEC~\Delta BFD\): \(\Rightarrow\)\(\frac{BE}{BF}\)\(\frac{BC}{B\text{D}}\)
Xét \(\Delta BEF\) Và \(\Delta BC\text{D}\) có :
\(\frac{BE}{BF}\)\(=\) \(\frac{BC}{B\text{D}}\)
\(\widehat{B}\) chung
\(\Rightarrow\) \(\Delta BEF\) \(~\) \(\Delta BC\text{D}\)( c - g - c )