Cho tam giác ABC vuông tại A và BD là đường phân giác trong. Từ D kẻ DE vuông góc với BC tại E. Các tia ED và BA cắt nhau tại F. Gọi I là trung điểm đoạn thảng CF.
a, Chứng minh DA=DE và DC>AF
b,Chứng minh B,D,I thẳng hàng
c,Gọi M là trung điểm FD. Chứng tỏ MA=MI
d,Chứng minh DB+DC+DF<FB+FC
Giúp mik nha, mai ktra rồi


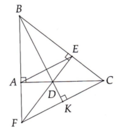
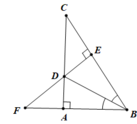
a, Xét 2 tam giác vuông ABD và EBD có:
BC cạnh chung
\(\widehat{ABD}\)=\(\widehat{EBD}\)(gt)
=> \(\Delta\)ABD=\(\Delta\)EBD(CH-GN)
=> DA=DE(2 cạnh tương ứng)
b, xét 2 tam giác vuông ADF và EDC có:
DA=DE(theo câu a)
\(\widehat{ADF}\)=\(\widehat{EDC}\)(vì đối đỉnh)
=> \(\Delta\)ADF=\(\Delta\)EDC(cạnh góc vuông-góc nhọn kề)
=> DF=DC mà DF>AF(cạnh huyền lớn hơn cạnh góc vuông) suy ra DC>AF
c, ta có \(\Delta\)FBI=\(\Delta\)CBI(c.c.c)
=> \(\widehat{FIB}\)=\(\widehat{CIB}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{FIB}\)=\(\widehat{CIB}\)= 90 độ
=> BI\(\perp\)CF
trong \(\Delta\)CFB có: CA,BI,FE là các đường cao cắt nhau tại D
=> B,D,I thẳng hàng
c,
mk ghi nhầm câu a, va câu b, (hai câu đó gộp lại thành 1)
còn câu c, là câu b,