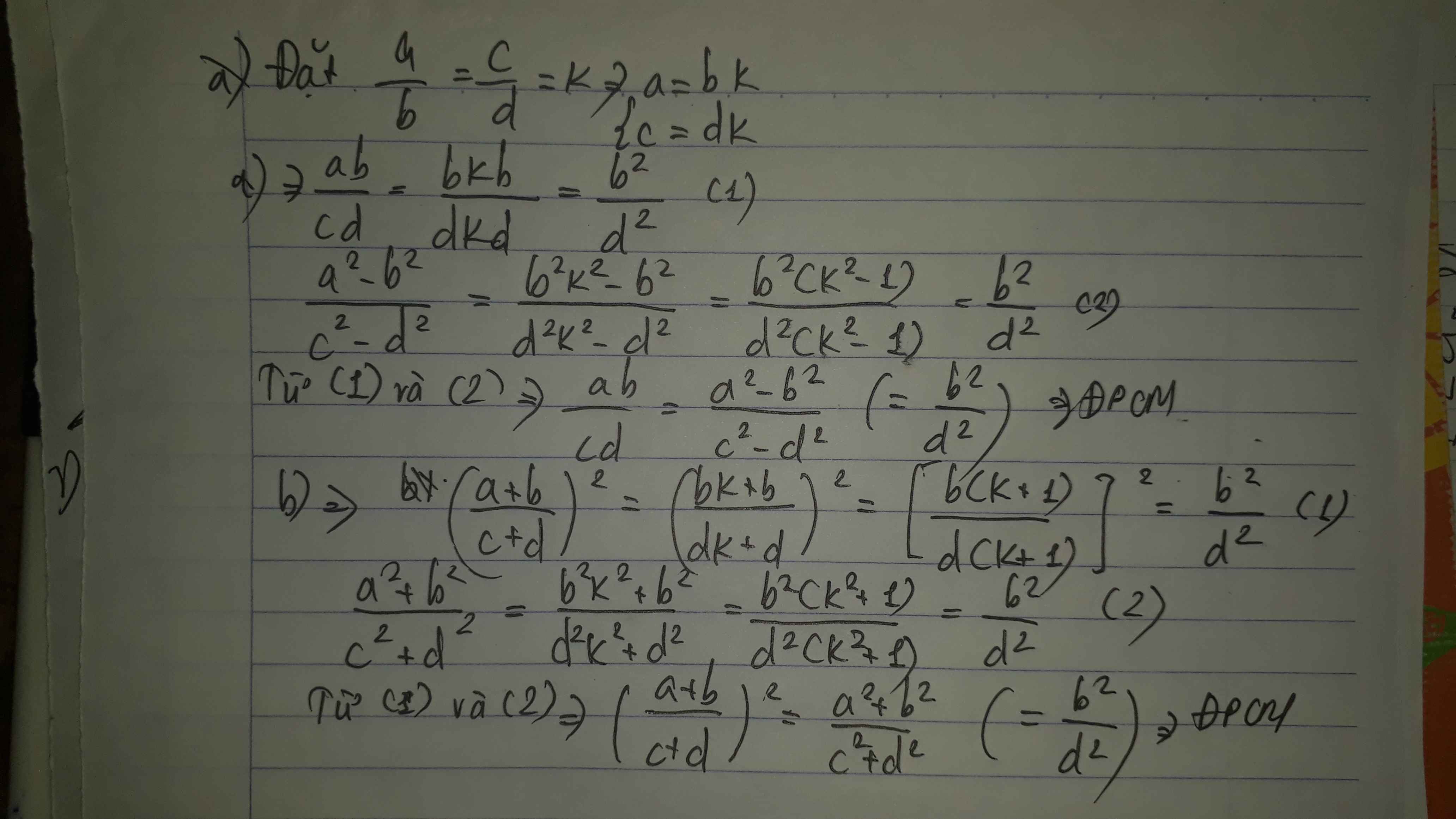Cho a/b=b/c=c/d, chứng minh (a+b+c/b+c+d)^4=ab/cd ( giả thiết các tỉ số đều có nghĩa)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 10 2016
Đặt \(\frac{a}{b}=\frac{c}{d}=k\) thì \(a=bk,c=dk\).
\(\frac{2a+3b}{2a-3b}=\frac{2bk+3b}{2bk-3b}=\frac{b\left(2k+3\right)}{b\left(2k-3\right)}=\frac{2k+3}{2k-3}\\ \frac{2c+3d}{2c-3d}=\frac{2dk+3d}{2dk-3d}=\frac{d\left(2k+3\right)}{d\left(2k-3\right)}=\frac{2k+3}{2k-3}\)
Do đó: \(\frac{2a+3b}{2a-3b}=\frac{2c+3d}{2c-3d}\)
5 tháng 11 2021
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2-c^2}{b^2-d^2}=k^2\)
\(\dfrac{ac}{bd}=k^2\)
Do đó: \(\dfrac{a^2-c^2}{b^2-d^2}=\dfrac{ac}{bd}\)
24 tháng 9 2017
Đặt :
\(\dfrac{a}{b}=\dfrac{c}{d}=k\)\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\d=ck\end{matrix}\right.\)
Ta có :
\(VT=\dfrac{ab}{cd}=\dfrac{bk.b}{dk.d}=\dfrac{b^2}{d^2}\left(1\right)\)
\(VP=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}=\dfrac{\left(bk+b\right)^2}{\left(dk+d\right)^2}=\dfrac{b^2+\left(k+1\right)^2}{d^2+\left(k+1\right)^2}=\dfrac{b^2}{d^2}\)\(\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrowđpcm\)
LV
24 tháng 9 2017
Gọi \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\)=k\(\Rightarrow\)\(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:\(\dfrac{ab}{cd}\)=\(\dfrac{bk.b}{dk.d}\)=\(\dfrac{b^2.k}{d^2.k}\)=\(\dfrac{b^2}{d^2}\)=\(\left(\dfrac{b}{d}\right)^2\)(vì k khác 0) 1
\(\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\)=\(\dfrac{\left(bk+b\right)^2}{\left(dk+d\right)^2}\)=\(\dfrac{\left[b.\left(k+1\right)\right]^2}{\left[d.\left(k+1\right)\right]^2}\)\(\left(\dfrac{b}{d}\right)^2\)=(vì k+1 khác 0) 2
Từ 1 và 2:
\(\Rightarrow\)\(\dfrac{ab}{cd}\)=\(\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\)
Vậy \(\dfrac{ab}{cd}\)=\(\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\)(điều cần chứng minh)
24 tháng 7 2019
a)\(\frac{ab}{cd}=\frac{bk.b}{dk.b}=\frac{b^2}{d^2}\left(1\right)\)
\(\frac{a^2-b^2}{c^2-d^2}=\frac{b^2k^2-b^2}{d^2k^2-d^2}=\frac{b^2\left(k^2-1\right)}{d^2\left(k^2-1\right)}=\frac{b^2}{d^2}\left(2\right)\)
từ\(\left(1\right)\)và\(\left(2\right)\)\(\Rightarrow\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\)
14 tháng 10 2021
a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{5b}{5d}=\dfrac{3a}{4c}=\dfrac{4b}{4d}=\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\Rightarrow\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
14 tháng 10 2021
c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}\)
\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\dfrac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\dfrac{b^2}{d^2}\)
Do đó \(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
d, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\)
\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\)
Do đó \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
DD
Đoàn Đức Hà
Giáo viên
2 tháng 10 2021
Đặt \(\frac{a}{b}=\frac{c}{d}=t\Rightarrow a=bt,c=dt\).
\(\frac{a-2c}{3a+c}=\frac{bt-2dt}{3bt+dt}==\frac{b-2d}{3b+d}\).