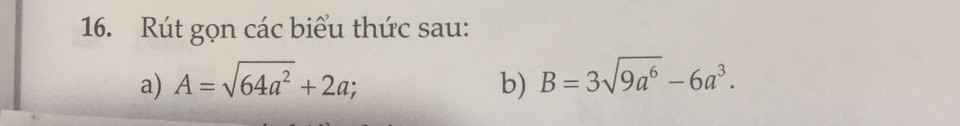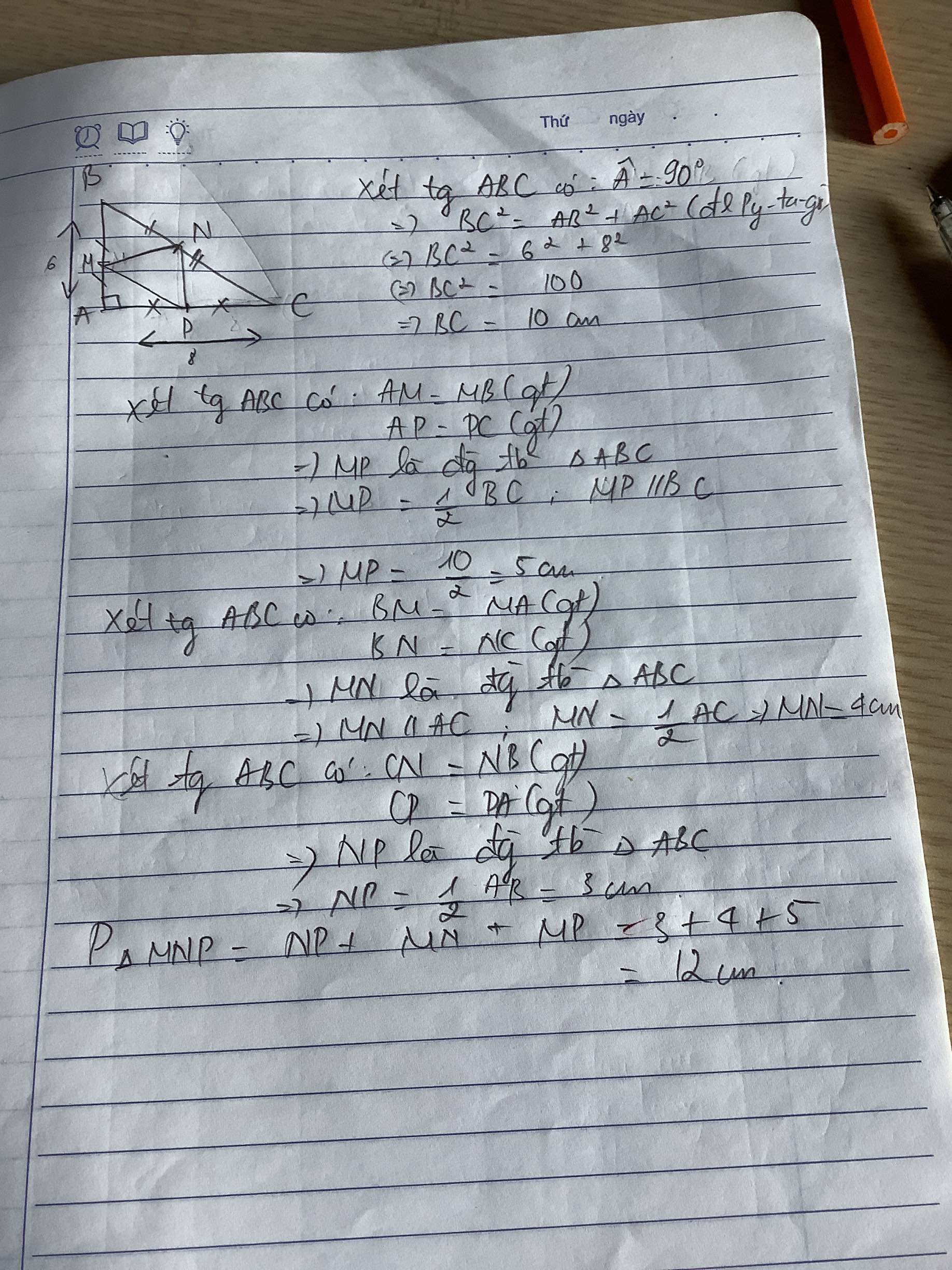Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(A=\sqrt{64a^2}+2a=8a+2a=10a\)
b: \(B=3\sqrt{9a^6}-6a^3=3\cdot3a^3-6a^3=3a^3\)
a) \(A=\sqrt{64a^2}+2a=8\left|a\right|+2a\)
b) \(B=3\sqrt{9a^6}-6a^3=9\left|a^3\right|-6a^3\)



Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=4\sqrt{41}\left(cm\right)\\AC=5\sqrt{41}\left(cm\right)\end{matrix}\right.\)

Bài 1:
c) (1) S+ O2 -> SO2
(2) SO2 + 2 NaOH -> Na2SO3 + H2O
(3) SO2 + 1/2 O2 \(⇌\left(to,xt\right)\) SO3
(4) SO3 + H2O -> H2SO4
(5) H2SO4 + 2 NaOH -> Na2SO4 +2 H2O
(6) Na2SO4 + BaCl2 -> BaSO4 + 2 NaCl
(7) SO3 ra chất gì mũi tên xuống?
(8) SO2 + H2O \(⇌\) H2SO3
(9) H2SO3+ Na2SO4 -> H2SO4 + Na2SO3
(10) Na2SO3+ H2SO4 -> Na2SO4 + SO2 + H2O
Bài 1:
a) (1) CaCO3 + Ba(OH)2 -> BaCO3 + Ca(OH)2
(2) CaCO3 -to-> CaO + CO2
(3) CaCO3 ra CaCO3?
(4) CaO + 2 HCl -> CaCl2 + H2O

a: \(=\dfrac{-14}{7}+\dfrac{4}{2}=-2+2=0\)
b: \(=\dfrac{1}{7}+\dfrac{6}{7}\cdot\dfrac{1}{6}=\dfrac{1}{7}+\dfrac{1}{7}=\dfrac{2}{7}\)

a: \(=\dfrac{-14}{7}+\dfrac{4}{2}=-2+2=0\)
b: \(=\dfrac{1}{7}+\dfrac{6}{7}\cdot\dfrac{1}{6}=\dfrac{1}{7}+\dfrac{1}{7}=\dfrac{2}{7}\)


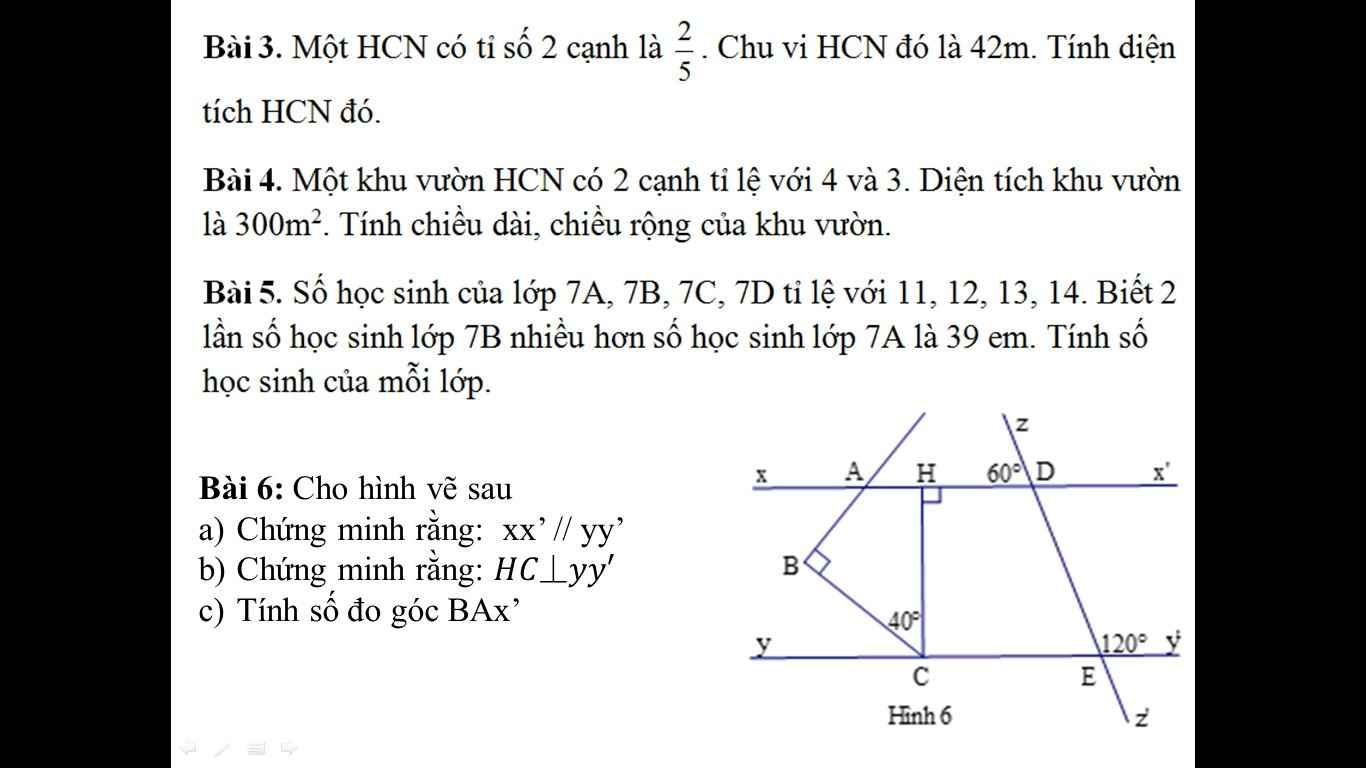
Bài 3:
Diện tích là:
\(15\cdot6=90\left(m^2\right)\)
Bài 3:
Gọi cd,cr lần lượt là a,b(m;a,b>0)
Áp dụng tc dtsbn:
\(\dfrac{b}{a}=\dfrac{2}{5}\Rightarrow\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a+2b}{10+4}=\dfrac{42}{14}=3\\ \Rightarrow\left\{{}\begin{matrix}a=15\\b=6\end{matrix}\right.\\ \Rightarrow S_{hcn}=ab=90\left(m^2\right)\)
Bài 4:
Gọi cd,cr lân lượt là a,b(m;a,b>0)
Đặt \(\dfrac{a}{4}=\dfrac{b}{3}=k\Rightarrow a=4k;b=3k\)
\(ab=300\left(m^2\right)\\ \Rightarrow12k^2=300\\ \Rightarrow k^2=25\Rightarrow k=5\left(k>0\right)\\ \Rightarrow\left\{{}\begin{matrix}a=20\\b=15\end{matrix}\right.\)
Vậy ...
Bài 5:
Gọi số hs 7A,7B,7C,7D ll là a,b,c,d(hs;a,b,c,d∈N*)
Áp dụng tc dtsbn:
\(\dfrac{a}{11}=\dfrac{b}{12}=\dfrac{c}{13}=\dfrac{d}{14}=\dfrac{2b-a}{24-11}=\dfrac{39}{13}=3\\ \Rightarrow\left\{{}\begin{matrix}a=33\\b=36\\c=39\\d=42\end{matrix}\right.\)
Vậy ...