Tìm x,y \(\in\)Z TM: x-2xy + y = 10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
15 tháng 4 2019
đỗ thị cẩm ly dạng này thì lớp 9 mới chính thức học,nhưng lớp 7 có thể đưa về những dạng quen thuộc để giải ạ.Vd: tìm x để biểu thức y nguyên
Lời giải
Theo đề bài,với x = 1 suy ra \(0y=3\) (vô lí)
Xét \(x\ne1\),chia hai vế của đẳng thức cho x - 1,được:
\(y=\frac{x^2+2}{x-1}=\frac{x^2-1^2}{x-1}+\frac{3}{x-1}\)
\(=\left(x+1\right)+\frac{3}{x-1}\)(dùng đẳng thức:\(a^2-b^2=\left(a-b\right)\left(a+b\right)\) ,tự chứng minh,sẽ ra được kết quả này)
Do x + 1 nguyên (với mọi x thuộc Z),nên để y thuộc Z(tức là y nguyên ấy)
Thì \(\frac{3}{x-1}\inℤ\Rightarrow x-1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
Suy ra \(x\in\left\{-2;0;2;4\right\}\).Thay từng giá trị của x vào \(y=\frac{x^2+2}{x-1}\) sẽ tìm được y (lưu ý đk y nguyên)
T
15 tháng 4 2019
Đầu tiên,xét bài toán phụ: CMR: \(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
Thật vậy,ta có: \(a^2-b^2=\left(a^2+ab\right)-\left(ab+b^2\right)\)
\(=a\left(a+b\right)-b\left(a+b\right)=\left(a-b\right)\left(a+b\right)\)
Trở lại bài toán,ta có \(y\left(x-1\right)-x^2=2\) (chuyển vế)
Thêm 12 vào mỗi vế và áp dụng quy tắc dấu ngoặc:
\(y\left(x-1\right)-\left(x^2-1^2\right)=3\)
\(\Leftrightarrow y\left(x-1\right)-\left(x-1\right)\left(x+1\right)=3\)
\(\Leftrightarrow\left(x-1\right)\left(y-x-1\right)=3\)
Dễ dàng nhận xét rằng \(x-1;y-x-1\inƯ\left(3\right)\)
Xét bốn trường hợp:
TH1: \(\hept{\begin{cases}x-1=-3\\y-x-1=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-2\\y=-2\end{cases}}\)
TH2: \(\hept{\begin{cases}x-1=-1\\y-x-1=-3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=-2\end{cases}}\)
TH3: \(\hept{\begin{cases}x-1=1\\y-x-1=3\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=6\end{cases}}\)
TH4; \(\hept{\begin{cases}x-1=3\\y-x-1=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=4\\y=6\end{cases}}\)
Vậy \(\left(x;y\right)=\left\{\left(-2;-2\right),\left(0;-2\right),\left(2;6\right),\left(4;6\right)\right\}\)
EC
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 11 2021
\(\Leftrightarrow\left(x^2+y^2+1-2xy+2x-2y\right)+\left(y^2-4y+4\right)=4\)
\(\Leftrightarrow\left(x-y+1\right)^2+\left(y-2\right)^2=4=2^2+0^2=0^2+2^2\)
\(\Rightarrow x;y\)
AH
Akai Haruma
Giáo viên
8 tháng 12 2021
1.
PT $\Leftrightarrow (x^2+2xy+y^2)-(y^2+6y+9)=0$
$\Leftrightarrow (x+y)^2-(y+3)^2=0$
$\Leftrightarrow (x+y-y-3)(x+y+y+3)=0$
$\Leftrightarrow (x-3)(x+2y+3)=0$
$\Rightarrow x-3=0$ hoặc $x+2y+3=0$
Nếu $x-3=0\Leftrightarrow x=3$. Vậy $(x,y)=(3,a)$ với $a$ nguyên bất kỳ.
Nếu $x+2y+3=0\Leftrightarrow x=-2y-3$ lẻ. Vậy $(x,y)=(-2a-3,a)$ với $a$ nguyên bất kỳ.
AH
Akai Haruma
Giáo viên
8 tháng 12 2021
2.
PT $\Leftrightarrow x^2=(y^2+2y+1)+12$
$\Leftrightarrow x^2=(y+1)^2+12\Leftrightarrow x^2-(y+1)^2=12$
$\Leftrightarrow (x-y-1)(x+y+1)=12$
Vì $x-y-1, x+y+1$ là số nguyên và cùng tính chẵn lẻ nên xảy ra các TH sau:
TH1: $x-y-1=2; x+y+1=6\Rightarrow x=4; y=1$
TH2: $x-y-1=6; x+y+1=2\Rightarrow x=4; y=-3$
TH3: $x-y-1=-2; x+y+1=-6\Rightarrow x=-4; y=-3$
TH4: $x-y-1=-6; x+y+1=-2\Rightarrow x=-4; y=1$
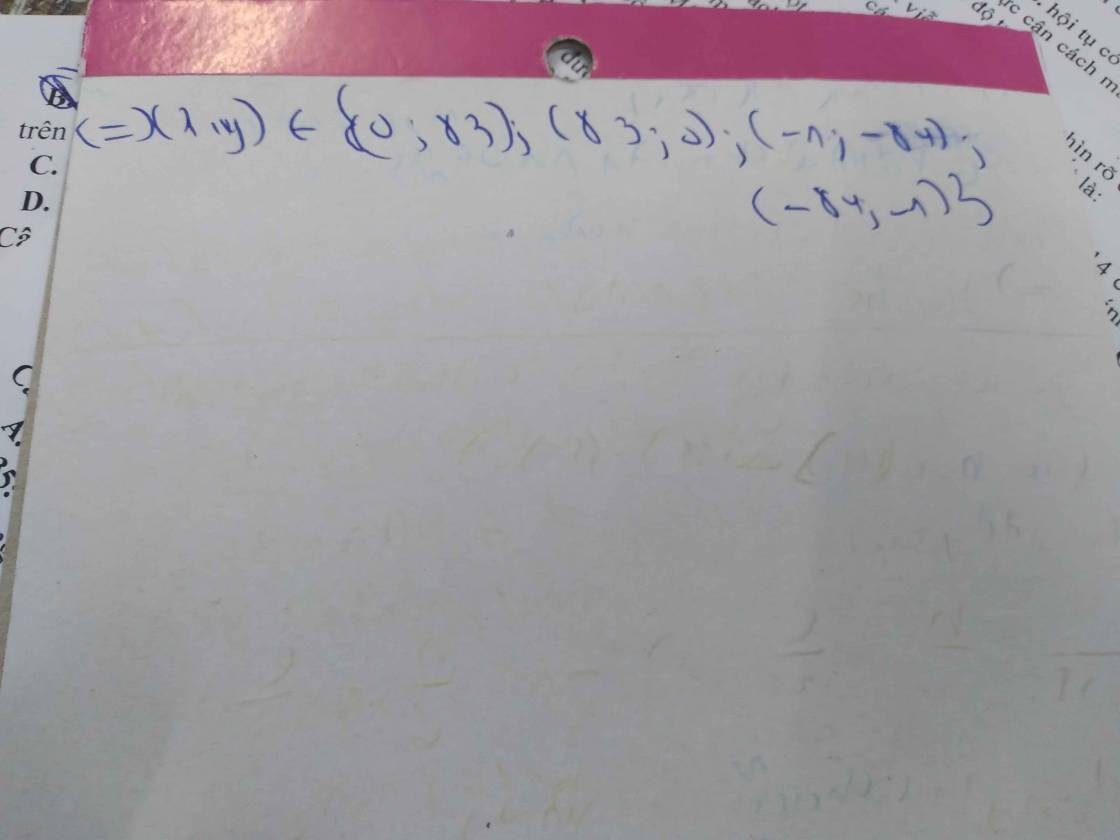
ĐỪNG ẤN ĐỌC THÊM.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
Đã kêu đừng ấn mà đéo nghe :))))
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.Thôi, lướt tiếp đi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
Lần này nữa thôi :)))
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.Cố lên
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
x - 2xy + y =10
=>2x - 4xy + 2y =20
=> 2x(1-2y) + 2y - 1=19
=> 2x (1-2y) -(1- 2y)=19
=>(2x-1).(1-2y)=19
vì x,y là các số nguyên nên (2x-1) và (1-2y) là các số nguyên do đó ta có các trường hợp sau:
\(\hept{\begin{cases}2x-1=1\\1-2y=19\end{cases}}\)hoặc \(\hept{\begin{cases}2x-1=19\\1-2y=1\end{cases}}\); \(\hept{\begin{cases}2x-1=-1\\1-2y=-19\end{cases}}\)hoặc \(\hept{\begin{cases}2x-1=-19\\1-2y=-1\end{cases}}\)
=> \(\hept{\begin{cases}x=1\\y=-9\end{cases}}\)hoặc \(\hept{\begin{cases}x=10\\y=0\end{cases}}\); \(\hept{\begin{cases}x=0\\y=10\end{cases}}\)hoặc \(\hept{\begin{cases}x=-9\\y=1\end{cases}}\)
vậy (x,y)\(\in\)(1,-9);(10,0);(0,10);(-9,1)