Cho \(\Delta ABC\) có AB = 9cm, AC = 12cm, BC = 15cma) \(\Delta ABC\)là \(\Delta\)gì? Vì sao?b) Vẽ trung tuyến AM của \(\Delta ABC\), lấy H là hình chiếu của M trên AC (H \(\in\)AC). Trên tia đối của tia MH lấy điểm K sao cho MK = MH. C/m: \(\Delta MHC=\Delta MKB\)và \(BK//AC\)c) Gọi G là giao điểm của BH và AM. C/m G là trọng tâm của \(\Delta...
Đọc tiếp
Cho \(\Delta ABC\) có AB = 9cm, AC = 12cm, BC = 15cm
a) \(\Delta ABC\)là \(\Delta\)gì? Vì sao?
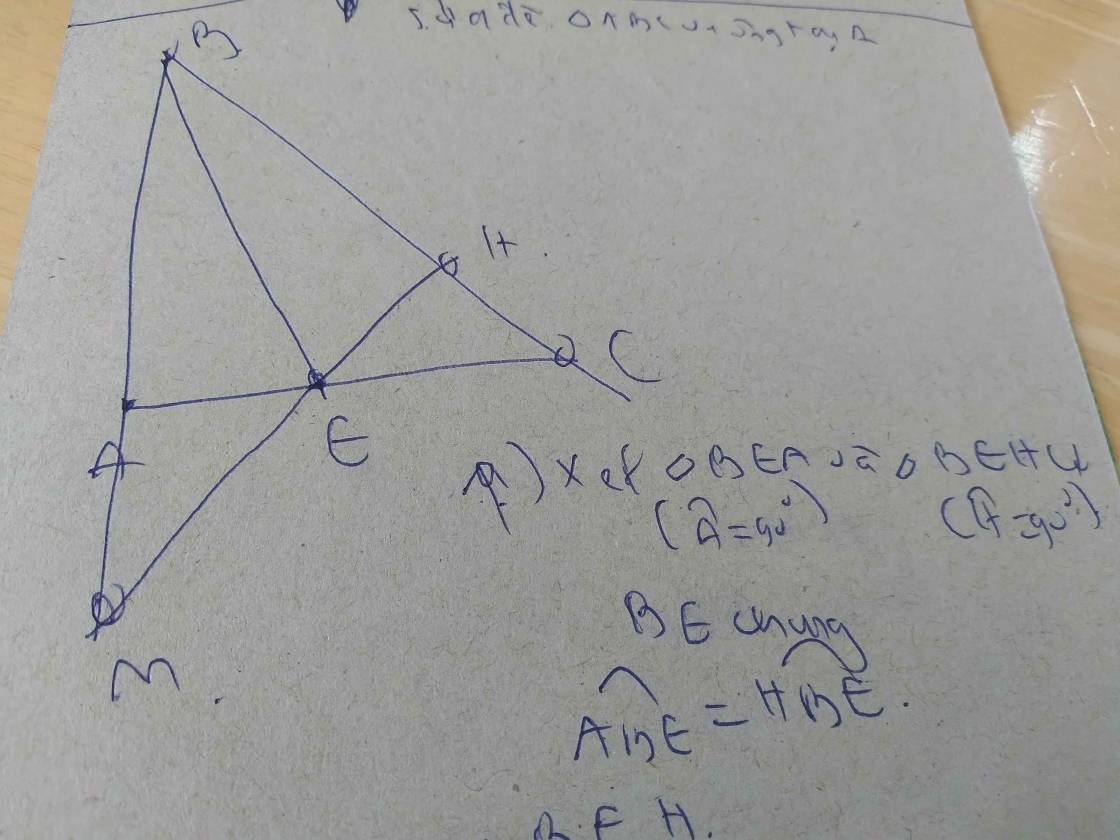
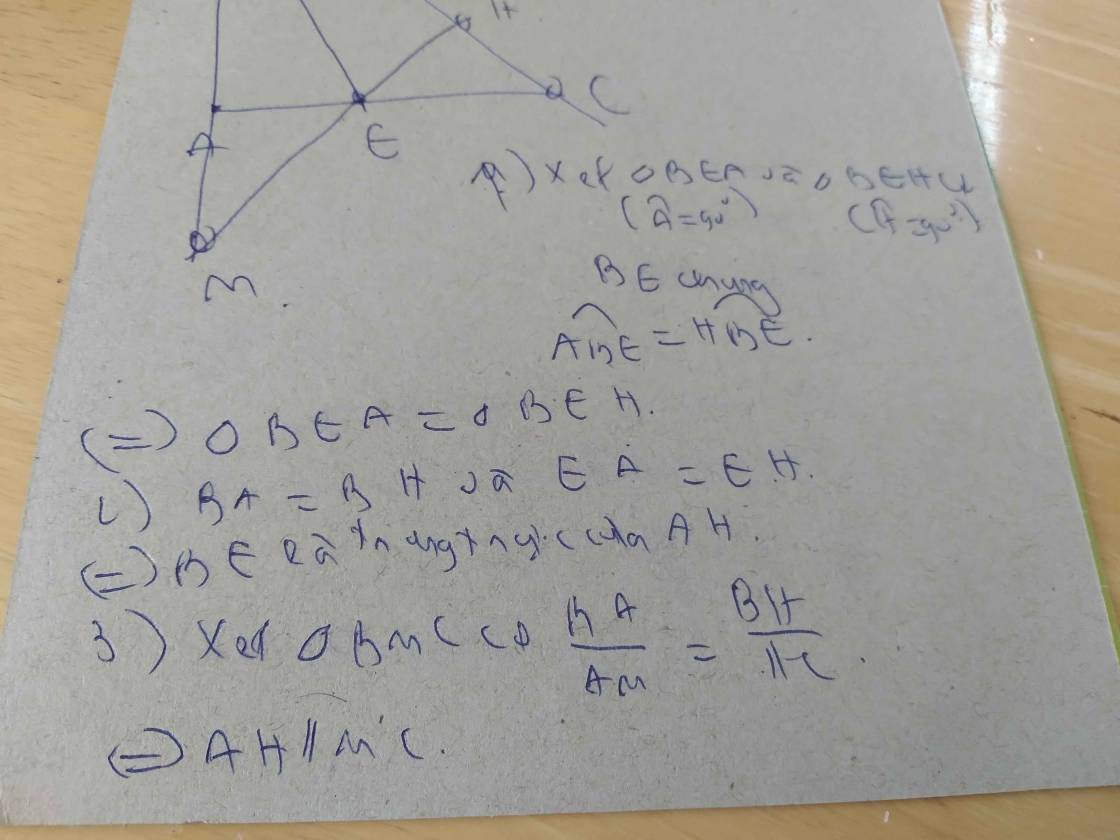
b) Vẽ trung tuyến AM của \(\Delta ABC\), lấy H là hình chiếu của M trên AC (H \(\in\)AC). Trên tia đối của tia MH lấy điểm K sao cho MK = MH. C/m: \(\Delta MHC=\Delta MKB\)và \(BK//AC\)
c) Gọi G là giao điểm của BH và AM. C/m G là trọng tâm của \(\Delta ABC\)
a) Theo định lí pytago vào tam giác ABC:
BC2=AB2+AC2
=>BC^2=9^2+12^2
=>BC^2=81+144
=>BC^2=225
=>BC^2=căn 225=15 cm.(theo giả thiết cho cũng bằng 15 cm)
Vậy tam giác ABC vuông tại A
b) Vì MH=MK mà MH vuông góc với AC, MK là tia đối của MH nên tam giác KMB vuông tại K
Xét 2 tam giác MHC và MKB có:
MH = MK theo giả thiết
MB = MC vì AM là trung tuyến ứng với với BC
góc H = góc K = 90 độ
=> 2 tam giác trên bằng nhau.(cạnh huyền-cạnh góc vuông)
=> góc KMB = góc HMC.
Mặt khác, hai góc KMB và HMC ở vị trí so le trong nên BK//HC hay BK//AC.(còn một cách cm nữa)
c) Xét hai tam giác vuông MHA và MHC có:
MH chung
MA=MC vì AM là trung tuyến ứng với BC
góc MHA = góc MHC = 90 độ
=> tam giác MHA = tam giác MHC. (cạnh huyền - cạnh góc vuông)
=> HA=HC
=> H là trung điểm của BC
=> BH là trung tuyến ứng với AC
Vì AM, BC là các trung tuyến mà hai trung tuyến này(AM, BC) cắt tại G nên G là trọng tâm của tam giác ABC
Ko có hình hả bn?