2018x2+x-2019=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 10 2019
Đáp án B
Từ giả thiết
2017 1 − y 2017 x = x 2 + 2018 1 − y 2 + 2018 ⇔ 2017 1 − y 1 − y 2 + 2018 = 2017 x x 2 + 2018 *
Xét hàm số f t = 2017 t t 2 + 2018 với t ∈ 0 ; 1
⇒ f ' t = 2017 t ln 2017 t 2 + 2018 + 2 t .2017 t > 0
⇒ f t đồng biến trên 0 ; 1 . Do đó (*) ⇔ 1 − y = x ⇔ x + y = 1.
Ta có: 0 ≤ x y ≤ x + y 2 4 = 1 4 . Đặt m = x y ∈ 0 ; 1 4 . Khi đó :
S = 16 x 2 y 2 + 34 x y + 12 y + x y + x 2 − 3 x y = 16 m 2 − 2 m + 12 = g m
Xét hàm g m trên đoạn
0 ; 1 4 ⇒ g ' m = 32 m − 2 → g ' m = 0 ⇔ m = 1 16
Lúc này
g 0 = 12 , g 1 4 = 25 2 , g 1 16 = 191 16 ⇒ M = 25 2 m = 191 16 ⇒ M + m = 391 16 .
CM
15 tháng 2 2017
Đáp án B
Từ giả thiết
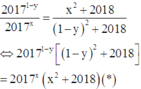
Xét hàm số
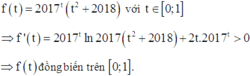
Do đó (*)
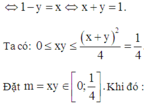
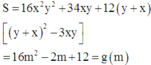
Xét hàm g(m) trên đoạn
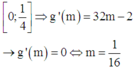
Lúc này
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2020
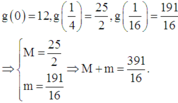
\(\Delta=1-4\left(3m-11\right)=-12m+45>0\Rightarrow m< \frac{15}{4}\)
Kết hợp Viet và điều kiện đề bài ta được:
\(\left\{{}\begin{matrix}x_1+x_2=1\\2017x_1+2018x_2=2019\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=1\\2017\left(x_1+x_2\right)+x_2=2019\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=-1\\x_2=2\end{matrix}\right.\)
Mà \(x_1x_2=3m-11\Leftrightarrow3m-11=-2\Rightarrow m=3\) (thỏa mãn)
15 tháng 11 2023
\(y=x^4-2018x^2-2019\) sẽ có TXĐ: D=R vì với mọi x thực thì y luôn xác định
PT
1
VK
2
12 tháng 8 2018
mk ko viết đề ra nhé
a,2019 x (1 + 99)
=2019 x 100
=201900
c,2018 x (7 + 1 + 2)
=2018 x 10
=20180
mk chỉ bk phần a và c thôi hihi
12 tháng 8 2018
a) \(2019+2019\times99=2019\times\left(1+99\right)=2019\times100=201900\)
b) \(\frac{7}{3}\times\frac{5}{9}+5\times\frac{3}{7}=\frac{35}{27}+\frac{15}{7}=\frac{650}{189}\)
c) \(2018\times7+2018+2018\times2=2018\times\left(7+1+2\right)=2018\times10=20180\)
d) \(\frac{225\times63}{9\times15}=\frac{15\times15\times9\times7}{9\times15}=15\times7=105\)
\(\Leftrightarrow2018x^2-2018x+2019x-2019=0\\ \Leftrightarrow2018x\left(x-1\right)+2019\left(x-1\right)=0\\ \Leftrightarrow\left(2018x+2019\right)\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\2018x=-2019\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{2019}{2018}\end{matrix}\right.\)