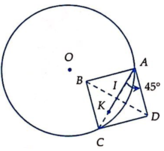
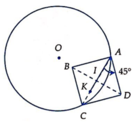
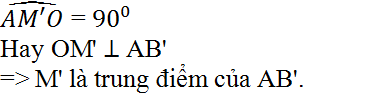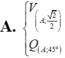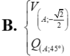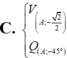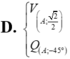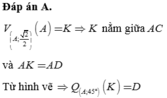Cho hình bình hành ABCD, hai điểm A, B cố định, tâm I di động trên đường tròn (C). Khi đó quỹ tích trung điểm M của cạnh BC:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


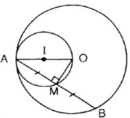
Phần thuận: giả sử M là trung điểm của dây AB. Ta có OM ⊥ AB (định lí)
Khi B di động trên (O), điểm M luôn nhình OA cố định dưới góc vuông , vậy M thuộc đường tròn đường kính OA.
Phần đảo: lấy điểm M' bất kì trên đường tròn đường kính OA.
Nối M' với A, đường thẳng M'A cắt đường tròn (O) tại B'. Nối M' với O ta có
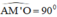
Hay OM' ⊥ AB'
⇒ M' là trung điểm của AB'
Kết luận: Tập hợp các trung điểm của dây AB là đường tròn đường kính OA.

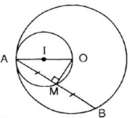
Phần thuận: giả sử M là trung điểm của dây AB. Ta có OM ⊥ AB (định lí)
Khi B di động trên (O), điểm M luôn nhình OA cố định dưới góc vuông , vậy M thuộc đường tròn đường kính OA.
Phần đảo: lấy điểm M' bất kì trên đường tròn đường kính OA.
Nối M' với A, đường thẳng M'A cắt đường tròn (O) tại B'. Nối M' với O ta có
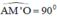
Hay OM' ⊥ AB'
⇒ M' là trung điểm của AB'
Kết luận: Tập hợp các trung điểm của dây AB là đường tròn đường kính OA.

Phần thuận: giả sử M là trung điểm của dây AB. Ta có OM ⊥ AB (định lí)
Khi B di động trên (O), điểm M luôn nhình OA cố định dưới góc vuông , vậy M thuộc đường tròn đường kính OA.
Phần đảo: lấy điểm M' bất kì trên đường tròn đường kính OA.
Nối M' với A, đường thẳng M'A cắt đường tròn (O) tại B'. Nối M' với O ta có

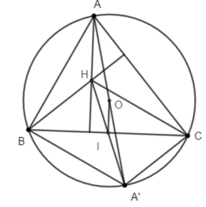
Gọi A’ là điểm đối xứng với A qua O. Ta có: BH // A’C suy ra BHCA’ là hình bình hành do đó HA’ cắt BC tại trung điểm I của BC. Mà O là trung điểm của AA’ suy ra OI là đường trung bình của tam giác AHA’ suy ra A H → = 2 O I →
Chọn đáp án C