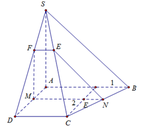
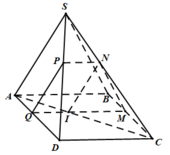
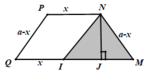
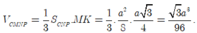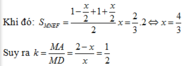Cho hình chóp S.ABCD với ABCD là hình thoi cạnh a. SAD là tam giác đều. Gọi M là một điểm thuộc cạnh AB, AM = x, (P) là mặt phẳng qua M // với (SAD). Tính diện tích thiết diện hình chóp cắt bởi mp (P).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
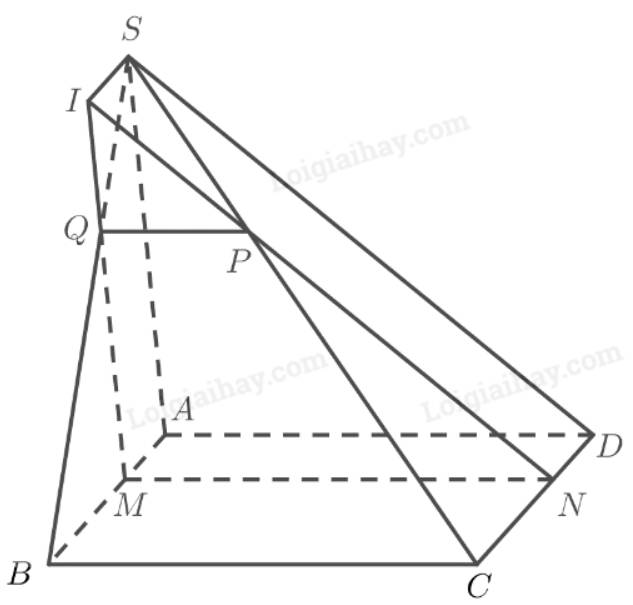
a) Ta có:
\(\left. \begin{array}{l}\left( \alpha \right) \cap \left( {SBC} \right) = PQ\\\left( \alpha \right) \cap \left( {ABCD} \right) = MN\\\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\end{array} \right\} \Rightarrow MN\parallel PQ\parallel BC\)
\( \Rightarrow MNPQ\) là hình thang (1).
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {SAB} \right) = MQ\\\left( {SA{\rm{D}}} \right) \cap \left( {SAB} \right) = SA\end{array} \right\} \Rightarrow MQ\parallel SA \Rightarrow \frac{{MQ}}{{SA}} = \frac{{BM}}{{AB}}\)
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {SC{\rm{D}}} \right) = NP\\\left( {SA{\rm{D}}} \right) \cap \left( {SC{\rm{D}}} \right) = SD\end{array} \right\} \Rightarrow NP\parallel SD \Rightarrow \frac{{NP}}{{SD}} = \frac{{CN}}{{C{\rm{D}}}}\)
\(\left. \begin{array}{l}\left( \alpha \right)\parallel \left( {SA{\rm{D}}} \right)\\\left( \alpha \right) \cap \left( {ABC{\rm{D}}} \right) = MN\\\left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = AD\end{array} \right\} \Rightarrow MN\parallel AD\parallel BC \Rightarrow \frac{{BM}}{{AB}} = \frac{{CN}}{{C{\rm{D}}}}\)
\( \Rightarrow \frac{{MQ}}{{SA}} = \frac{{NP}}{{S{\rm{D}}}}\)
Mà tam giác \(SAD\) đều nên \(SA = S{\rm{D}}\)
\( \Rightarrow MQ = NP\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow MNPQ\) là hình thang cân.
b) Gọi \(I = MQ \cap NP\). Ta có:
\(\left. \begin{array}{l}\left( {SAB} \right) \cap \left( {SA{\rm{D}}} \right) = SI\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SC{\rm{D}}} \right) \cap \left( {ABCD} \right) = C{\rm{D}}\end{array} \right\} \Rightarrow SI\parallel AB\parallel C{\rm{D}}\)
\(SI\parallel N{\rm{D}},S{\rm{D}}\parallel NI \Rightarrow SIN{\rm{D}}\) là hình bình hành \( \Rightarrow S{\rm{D}} = NI\)
\(SI\parallel MA,S{\rm{A}}\parallel MI \Rightarrow SIMA\) là hình bình hành \( \Rightarrow S{\rm{A}} = MI\)
Xét tam giác \(IMN\) và tam giác \(SAD\) có: \(MN\parallel A{\rm{D,}}MI\parallel SA,NI\parallel S{\rm{D}},MN = A{\rm{D}}\)
tam giác \(IMN\) là tam giác đều cạnh \(a\).
\(\begin{array}{l}SI\parallel AB \Rightarrow \frac{{SI}}{{BM}} = \frac{{IQ}}{{QM}} \Leftrightarrow \frac{{SI}}{{BM + SI}} = \frac{{IQ}}{{QM + IQ}} \Leftrightarrow \frac{{SI}}{{BM + MA}} = \frac{{IQ}}{{QM + IQ}}\\ \Leftrightarrow \frac{{SI}}{{AB}} = \frac{{IQ}}{{MI}} \Leftrightarrow IQ = \frac{{SI.MI}}{{AB}} = \frac{{x.a}}{a} = x\end{array}\)
\({S_{IMN}} = \frac{{{a^2}\sqrt 3 }}{4},{S_{IPQ}} = \frac{{{x^2}\sqrt 3 }}{4} \Rightarrow {S_{MNPQ}} = {S_{IMN}} - {S_{IPQ}} = \frac{{{a^2}\sqrt 3 }}{4} - \frac{{{x^2}\sqrt 3 }}{4} = \frac{{\sqrt 3 }}{4}\left( {{a^2} - {x^2}} \right)\)
CM
16 tháng 3 2018
Chọn B.
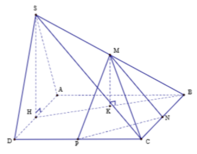
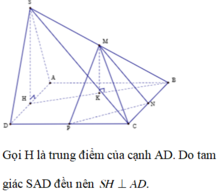
Gọi H là trung điểm của cạnh AD. Do tam giác SAD đều nên SH ⊥ AD
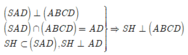
Gọi K là trung điểm của HB => MK//SH
Do đó: MK ⊥ ABCD => MK ⊥ (CNP).
Vậy MK là chiều cao của khối tứ diện CMNP.
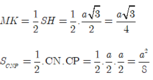
Thể tích khối tứ diện CMNP là
