Cho tam giác ABC hai tia phân giác của góc A và góc C cắt cạnh BC và BA lần lượt ở A' và C' và cắt nhau ở I. Chứng minh:
a) tứ giác BA'IC' nội tiếp
b) tam giác A'IC' cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 12 2020
sai ở đâu vậy ạ bạn cho mình xin ý kiến . Cảm ơn !
mình không biết mình có ns sai hay đúng nhưng nếu vẽ hình thì BC không bằng BD . Mong bạn giúp
R
31 tháng 1 2022
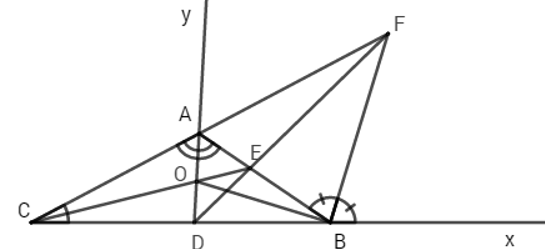
a) Xét \(\Delta ABC\) có tia phân giác \(BAC,ACB\) cắt nhau tại O suy ra O là giao điểm của 3 đường phân giác trong tam giác ABC suy ra BO là phân giác của \(\widehat{CBA}\) (tính chất 3 đường phân giác của tam giác)
\(\Rightarrow DBO=ABO=\dfrac{DBA}{2}\left(1\right)\) ( tính chất tia phân giác )
Lại có BF là phân giác của \(\widehat{ABx\left(gt\right)}\) \(=ABF=FBx\left(2\right)\)
( tính chất của tia phân giác )
Mà \(ABD+ABx=180^o\left(3\right)\left(kềbu\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow OBA+ABF=180^o\div2=90^o\Rightarrow BO\text{⊥ }BF\)
b) Ta có \(FAB+BAC=180^o\)( kề bù ) mà \(BAC=120^o\left(gt\right)\Rightarrow FAB=60^o\)
\(\Rightarrow\text{AD là phân giác của}\widehat{BAC}\) ( dấu hiệu nhận biết tia phân giác )
\(\Rightarrow BAD=CAD=60^o\) ( tính chất tia phân giác )
\(\Rightarrow FAy=CAD=60^o\) ( đối đỉnh ) \(\Rightarrow FAB=FAy=60^o\Rightarrow\) AF là tia phân giác của \(BAy\) ( dấu hiệu nhận biết tia phân giác )
Vậy \(\Delta ABD\) có hai tia phân giác của hai góc ngoài tại đỉnh A và đỉnh B cắt nhau tại F nên suy ra DF là phân giác của \(ADB=BDF=ADF\) ( tính chất tia phân giác )
c) Xét \(\Delta ACD\) có phân giác góc ngoài tại đỉnh A và phân giác trong tại đỉnh C cắt nhau tại E nên suy ra DE cũng là phân giác của \(ADB\Rightarrow\)\(D,E,F\) thẳng hàng
31 tháng 1 2022
thật là ngược mộ nha
dù không biết đúng hay sai nhưng lâu lắm mới thấy người làm nguyên một bài toán hình thế này mà còn có hình nữa
KK
25 tháng 11 2018
a. Theo đề bài nên
Vì và nên
Suy ra hay
Trên cạnh AC lấy điểm K sao cho AE = AK
Hai tam giác AOE và AOK có:
AE = AK
(giả thiết)
AO là cạnh chung
Vậy
b. Ta có nên
OE = OK và
Mà góc AOE kề bù với góc DOE nên
Suy ra
Hai tam giác COK và COD có:
OC là cạnh chung
(giả thiết)
Vậy (g.c.g)
Suy ra OK = OD
Ở trên ta đã có OE = OK
Vậy OE = OK = OD