Cho tam giác ABC vuông tại A , M là trung điểm AC gọi EF theo thứ tự là chân đường vuông góc kẻ từ A và C đến BM
a, so sánh AC với tổng AC+EF
b, chứng minh:AB>BE-BF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
O
10 tháng 5 2017
Trong tam giác vuong ABC co
AC^2+AB^2=BC^2 (PYTAGO)
\(\Rightarrow9^2+12^2=BC^2\)
\(\Leftrightarrow BC^2=81+144\)
\(\Leftrightarrow BC^2=225\)
\(\Rightarrow BC=15\)
Xét 2 tam giác vuông\(\Delta MEA\)và\(\Delta MCF\)có
góc FMC= Góc EMA ( đối đỉnh)
AM=MC (gt)
\(\Rightarrow\Delta MEA=\Delta MCF\)( cảnh huyền - góc nhọn)
mình mới làm xong phần b thôi
4 tháng 5 2020
chín phần hai mươi đề xi mét khối băng bao nhiêu xăng ti mét khối
Vì sao?
CM
4 tháng 10 2017
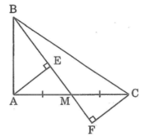
Trong ΔABM, ta có ∠(BAM) = 90o
Suy ra: AB < BM (trong tam giác vuông cạnh huyền lớn nhất)
Mà BM = BE + EM = BF - MF
Suy ra: AB < BE + EM
AB < BF - FM
Suy ra:AB + AB < BE + ME + BF - MF (1)
Xét hai tam giác vuông AEM và CFM, ta có:
∠(AEM) = ∠(CFM) = 90o
AM = CM (gt)
∠(AME) = ∠(CMF) (đối đỉnh)
Suy ra: ΔAEM = ΔCFM (cạnh huyền - góc nhọn)
Suy ra: ME = MF (2)
Từ (1) và (2) suy ra: AB + AB < BE + BF
Suy ra: 2AB < BE + BF
Vậy AB < (BE + BF) / 2 .
9 tháng 7 2021
a) Xét tứ giác AEMF có
\(\widehat{AFM}=90^0\)(gt)
\(\widehat{AEM}=90^0\)(gt)
\(\widehat{FAE}=90^0\)(gt)
Do đó: AFME là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: AM=EF(Hai đường chéo của hình chữ nhật AFME)
b) Gọi O là giao điểm của AM và EF
Ta có: AMFE là hình chữ nhật(cmt)
nên Hai đường chéo AM và EF cắt nhau tại trung điểm của mỗi đường và bằng nhau(Định lí hình chữ nhật)
mà O là giao điểm của AM và EF(gt)
nên O là trung điểm của AM; O là trung điểm của EF
Ta có: ΔAHM vuông tại H(gt)
mà HO là đường trung tuyến ứng với cạnh huyền AM(O là trung điểm của AM)
nên \(HO=\dfrac{AM}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà AM=EF(cmt)
nên \(HO=\dfrac{EF}{2}\)
Xét ΔHFE có
HO là đường trung tuyến ứng với cạnh EF(O là trung điểm của EF)
\(HO=\dfrac{EF}{2}\)(cmt)
Do đó: ΔHFE vuông tại H(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)
23 tháng 3 2016
định lý thường nói : nếu trong 1 tam giác có tông độ dài hai cạnh luôn luôn lớn hơn cạnh còn lại
bạn dựa vào định lý đó để chứng minh
thanks