Một dây dẫn đồng chất có chiều dài l, tiết diện đều S có điện trở là 8Ω được gập đôi thành một dây dẫn mới có chiều dài l2l2. Điện trở của dây dẫn mới này là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
6 tháng 10 2019
Chọn D
Khi gập đôi sợi dây thì dây mới có chiều dài giảm đi 2 lần và tiết diện tăng gấp 2 lần. Chiều dài giảm 2 lần nên điện trở giảm hai lần, tiết diện tăng 2 lần nên điện trở giảm thêm 2 lần nữa kết quả là giảm 4 lần. Vì vậy điện trở dây dẫn mới là 8:4 = 2Ω.
VT
31 tháng 1 2017
Do dây dẫn được gập đôi lại nên chiều dài giảm đi 2 lần và tiết diện tăng 2 lần.
Chiều dài giảm 2 lần nên điện trở giảm 2 lần, tiết diện tăng 2 lần nên điện trở giảm 2 lần. Kết quả là giảm 4 lần.
Vì vậy điện trở dây dẫn mới là: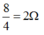 
→ Đáp án D
8 tháng 12 2021
Ta có: \(R=\rho\cdot\dfrac{l}{S}\)
Mà \(R'=\rho\cdot\dfrac{l'}{S}=\rho\cdot\dfrac{\dfrac{l}{2}}{S}=\dfrac{1}{2}R\)
\(\Rightarrow R'=\dfrac{1}{2}\cdot12=6\Omega\)
1 tháng 1 2021
Chiều dài dây dẫn được gấp ba thành dây dẫn có chiều dài L/3 đồng thời tiết diễn dây đó cũng tăng lên 3 lần
Giá trị điện trở của dây dẫn mới:
\(\dfrac{R_1}{R_2}=\dfrac{\dfrac{\rho.l}{S}}{\dfrac{\dfrac{\rho.l}{3}}{3S}}=9\)
\(\Rightarrow R_2=\dfrac{R_1}{9}=\dfrac{18}{9}=2\Omega\)
3 tháng 10 2021
Ta có: \(\dfrac{R}{R'}=\dfrac{\dfrac{p.l}{S}}{\dfrac{p.l'}{S}}=\dfrac{l}{l'}=\dfrac{l}{\dfrac{1}{2}l}=2\Rightarrow R'=\dfrac{R}{2}=\dfrac{8}{2}=4\left(\Omega\right)\)
15 tháng 12 2021
\(R_2=\rho\dfrac{l_2}{S_2}\Rightarrow\rho=\dfrac{R_2.S_2}{l_2}=\dfrac{8.0,1.10^{-6}}{10}=8.10^{-8}\left(\Omega.m\right)\)
\(R_1=\rho\dfrac{l_1}{S_1}=8.10^{-8}.\dfrac{20}{0,4.10^{-6}}=4\left(\Omega\right)\)
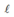
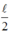
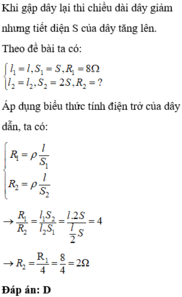
Cám ơn nè