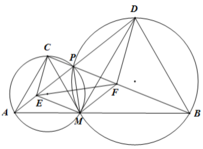
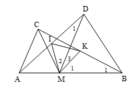
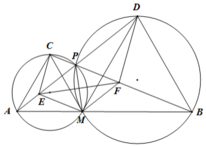
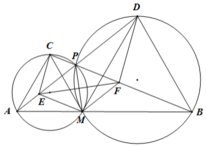
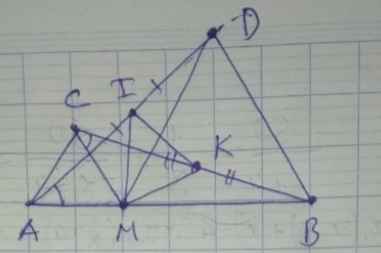
Cho đoạn thẳng AB cố định. Điểm M thay đổi trên đoạn thẳng AB. Dựng về một phía của đường thẳng AB hai tam giác đều AMC và BMD. Gọi P là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC
b) Các tứ giác AMPC và BMPD nội tiếp
c) PM là phân giác của góc APB
d) BC.BP + AD.AP = \(AB^2\)