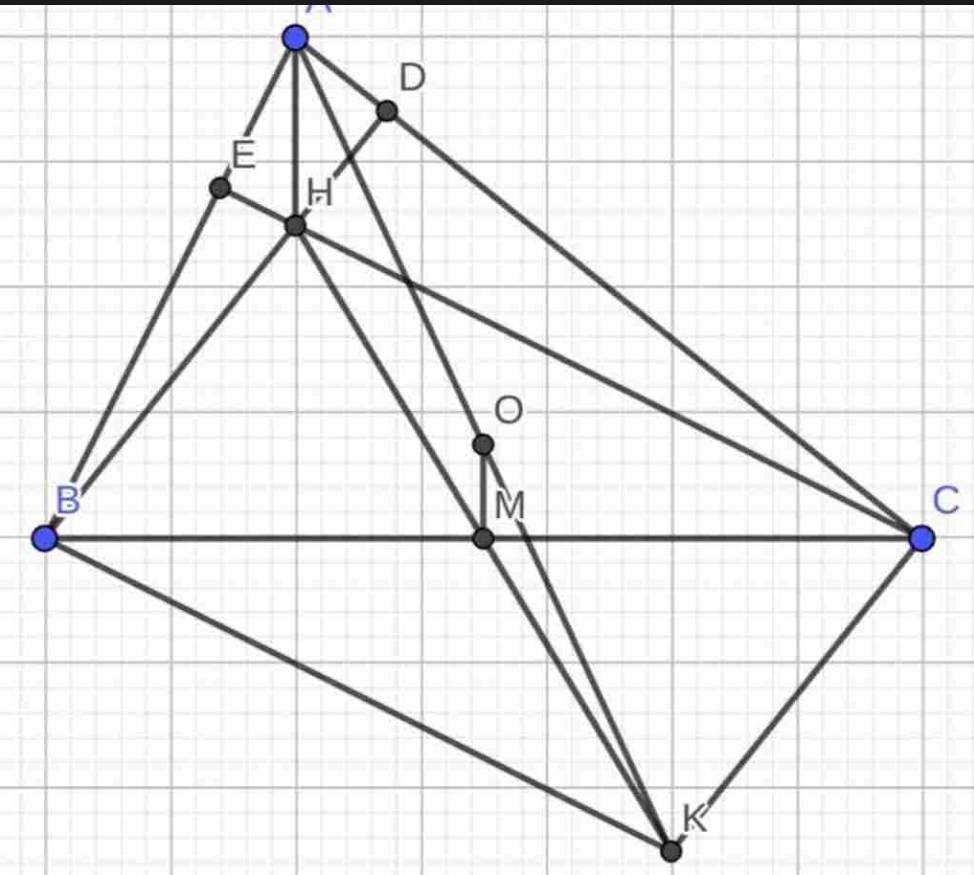
Cho \(\Delta ABC\)nhọn , có đường cao BD , CE cắt nhau tại H . Đường vuông góc với AB tại F và đường vuông góc với AC tại D cắt nhau tại K. M là trung điểm của BC .
a) Cm: \(\Delta ADB~\Delta AEC\)và \(\Delta AED~\Delta ACB\)
b) HI . HC = HD . HB
c) AH cắt BC cắt tại O . Cm : \(BE.BA+CD.CA=BC^2\)
d) \(\frac{HO}{AO}+\frac{HD}{BD}+\frac{HE}{CE}=1\)