Cho đường tròn (O) có dây AB khác đường kính. Điểm C bất kì trên AB và D bất kì trên cung nhỏ AB. Tia OC cắt đường tròn (OAB) tại F khác O. Đoạn OD cắt AB tại E. Đường thẳng FE cắt (OAB) tại G khác F. Tia GD cắt lại (OAB) ở Q. Chứng minh OQ chia đôi CD ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc AEB=1/2*180=90 độ
góc FIB+góc FEB=180 độ
=>FIBE nội tiếp
b: góc ACB=1/2*180=90 độ
=>AC vuông góc DB
Xét ΔCAF và ΔCEA có
góc CAF=góc CEA
góc ACF chung
=>ΔCAF đồng dạng với ΔCEA
=>CA^2=AF*AE
Xét ΔDAB vuông tại D có AC vuông góc DB
nên CA^2=CD*CB=AF*AE

2: I nằm trên trung trực của EF
=>IE=IF
=>góc IEF=góc IFE=góc OKE
=>IF//OK
=>IF vuông góc AB tại F
=>AB là tiêp tuyến của (I;IE)

góc AEK=góc ABK=1/2*sđ cung AK
góc AEK=góc BEK
=>sđ cung AK=sđ cung BK
=>góc AEK=1/2*sđ cung BK=góc BAK

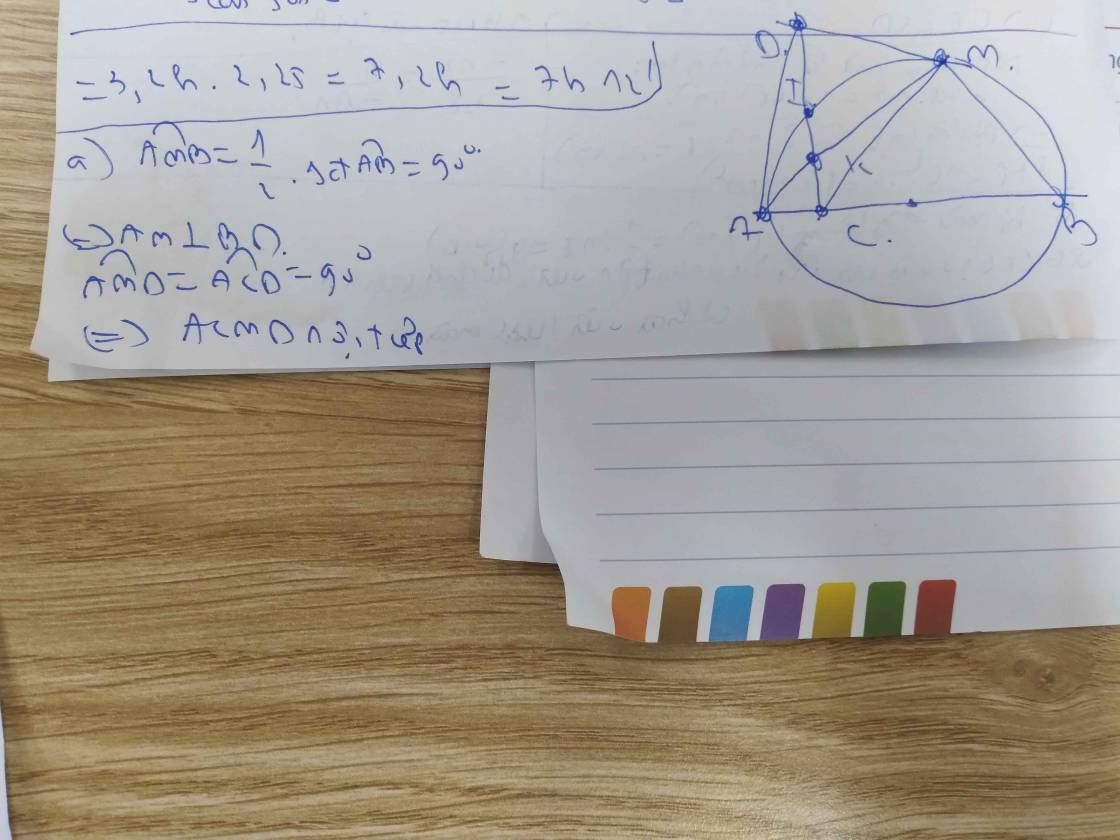
a: C là điểm chính giữa của cung AB
=>OC vuông góc AB tại I
=>CD là đường kính của (O)
góc CMD=1/2*sđ cung CD=90 độ
góc EMD+góc EID=180 độ
=>EMDI nội tiếp
b: Xét ΔCBE và ΔCMB có
góc BCE chung
góc CBE=góc CMB
=>ΔCBE đồng dạng với ΔCMB
=>CB/CM=CE/CB
=>CB^2=CM*CE
=>góc CBE=góc CMB
=>CB là tiếp tuyến của đường tròn ngoại tiếp ΔBME

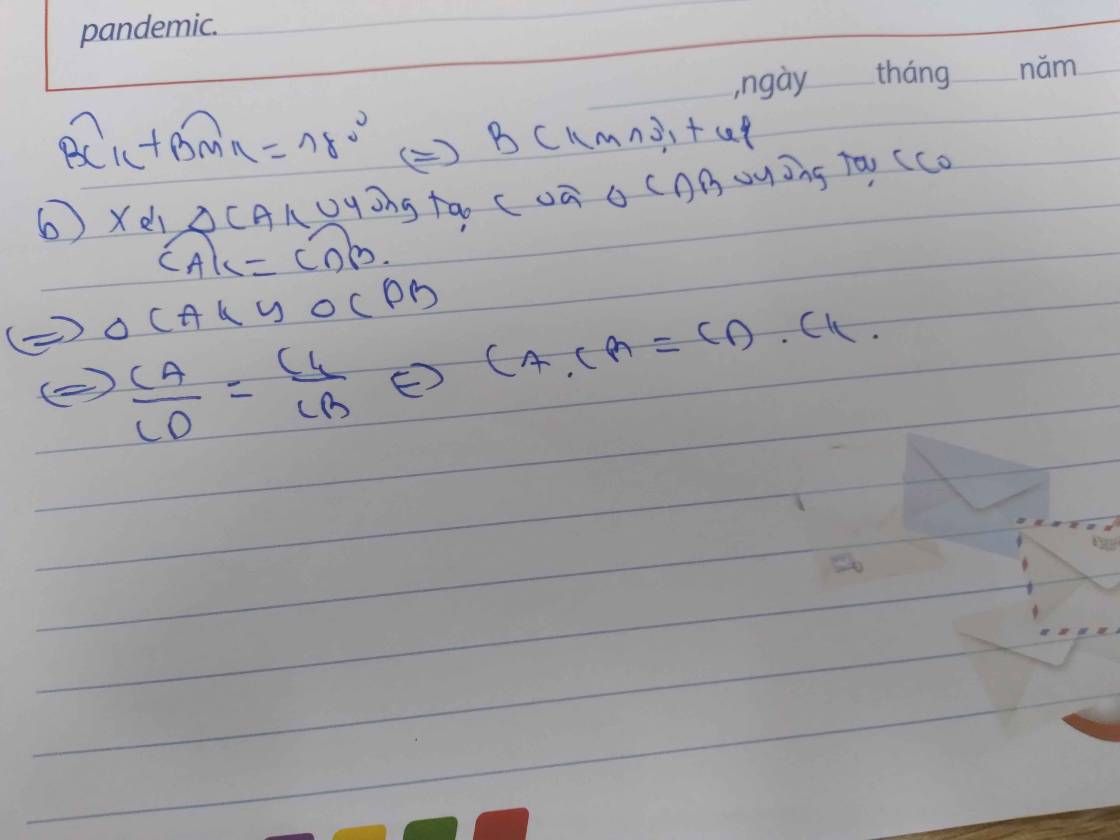
Gọi R đối xứng với D qua O. Khi đó DR là đường kính của (O) hay O là trung điểm RD.
Ta có: ^OBC = ^BFO (2 góc nội tiếp chắn (OA=(OB ) nên \(\Delta\)OCB ~ \(\Delta\)OBF (g,g)
Suy ra: OB2 = OC.OF hay OR2 = OC.OF. Từ đó: \(\Delta\)OCR ~ \(\Delta\)ORF (c.g.c) => ^ORC = ^OFR
Áp dụng hệ thức lượng đường tròn có: EG.EF = EA.EB = ED.ER nên tứ giác GDFR nội tiếp
Suy ra: ^OFR = ^GFR - ^GFO = ^GDR - ^GQO = ^DOQ. Từ đấy: ^ORC = ^DOQ
Do đó: CR // OQ. Xét trong \(\Delta\)DRC thấy: O trung điểm RD và OQ // CR cho nên OQ đi qua trung điểm CD (đpcm).