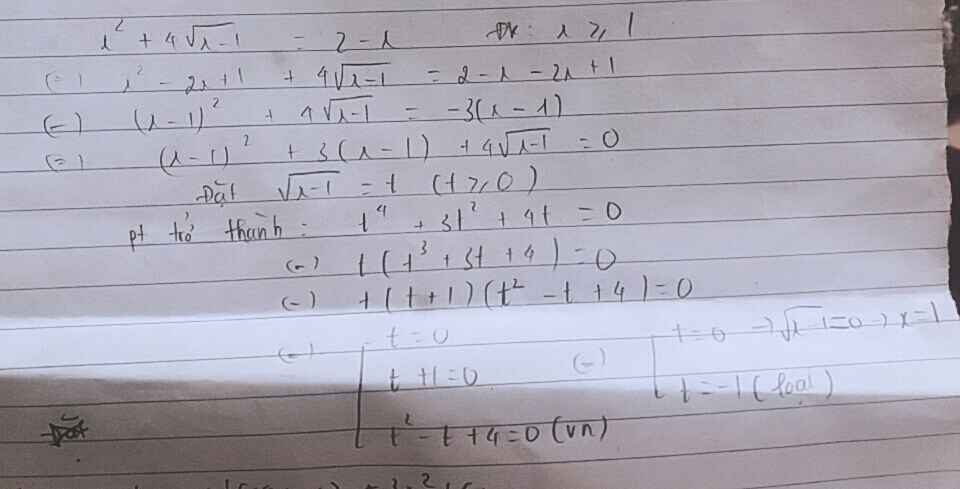Giải pt:
\(x^2+4\sqrt{x-1}=2-x\)
Giúp mình nhanh nkaaa.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ \(2\left(x^2-3x+2\right)=3\sqrt{x^3+8}\)
\(\Rightarrow2x^2-6x+4=3\sqrt{\left(x+2\right)\left(x^2-2x+4\right)}\)
\(\Rightarrow\left(-2\right)\left(x+2\right)+2\left(x^2-2x+4\right)=3\sqrt{\left(x+2\right)\left(x^2-2x+4\right)}\)
Chia 2 vế cho x2 - 2x + 4 ta được:
\(\left(-2\right).\frac{x+2}{x^2-2x+4}+2=3\sqrt{\frac{x+2}{x^2-2x+4}}\)
Đặt \(a=\sqrt{\frac{x+2}{x^2-2x+4}}\left(a\ge0\right)\) ta được:
\(-2a^2-3a+2=0\Rightarrow\left(1-2a\right)\left(a+2\right)=0\Rightarrow\orbr{\begin{cases}a=\frac{1}{2}\left(n\right)\\a=-2\left(l\right)\end{cases}}\)
\(a=\frac{1}{2}\Leftrightarrow\sqrt{\frac{x+2}{x^2-2x+4}}=\frac{1}{2}\Rightarrow\frac{x+2}{x^2-2x+4}=\frac{1}{4}\)
\(\Rightarrow x^2-6x-4=0\Rightarrow\orbr{\begin{cases}x=3+\sqrt{13}\\x=3-\sqrt{13}\end{cases}}\) (cái này tính denta là ra kết quả thôi)
Vậy có 2 nghiệm trên
câu b, c tương tự thôi


Mình làm câu 2 trước nhé:
đkxđ: \(\dfrac{1}{2}< x\le2\)
Áp dụng BĐT Bunyakovsky, ta có \(VT=\left(1.\sqrt{x}+1.\sqrt{2-x}\right)\)\(\le\sqrt{\left(1^2+1^2\right)\left[\left(\sqrt{x}\right)^2+\left(\sqrt{2-x}\right)^2\right]}\) \(=2\). ĐTXR \(\Leftrightarrow x=2-x\Leftrightarrow x=1\) (nhận). Vậy \(VT\le2\) (1)
Mặt khác, ta có \(\left(x-1\right)^2\ge0\) \(\Leftrightarrow x^2-\left(2x-1\right)\ge0\) \(\Leftrightarrow\left(x-\sqrt{2x-1}\right)\left(x+\sqrt{2x-1}\right)\ge0\). Do \(x+\sqrt{2x-1}>0\) nên điều này có nghĩa là \(x\ge\sqrt{2x-1}\) \(\Rightarrow\dfrac{x}{\sqrt{2x-1}}\ge1\) \(\Leftrightarrow\dfrac{2x}{\sqrt{2x-1}}\ge2\) hay \(VP\ge2\) (2). ĐTXR \(\Leftrightarrow x=1\) (nhận)
Từ (1) và (2) suy ra \(VT\le2\le VP\), do đó pt đã cho \(\Leftrightarrow VT=VP\) \(\Leftrightarrow x=1\)
Vậy pt đã cho có nghiệm duy nhất \(x=1\)

Bạn tham khảo lời giải tại đây:
https://hoc24.vn/cau-hoi/giai-pt-sqrtx-2sqrt4-x2x2-5x-1.219493072549

Đề đúng nhé các bạn. Bài này phải sử dụng pp hàm số mới đc. có thể vô ngiệm hoặc nghiệm xấu đấy

a)\(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
\(pt\Leftrightarrow\sqrt{3x^2+6x+3+4}+\sqrt{5x^2+10x+5+9}=-x^2-2x+4\)
\(\Leftrightarrow\sqrt{3\left(x^2+2x+1\right)+4}+\sqrt{5\left(x^2+2x+1\right)+9}=-x^2-2x+4\)
\(\Leftrightarrow\sqrt{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}=-x^2-2x+4\)
Dễ thấy: \(\hept{\begin{cases}3\left(x+1\right)^2\ge0\\5\left(x+1\right)^2\ge0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}3\left(x+1\right)^2+4\ge4\\5\left(x+1\right)^2+9\ge9\end{cases}}\)\(\Rightarrow\hept{\begin{cases}\sqrt{3\left(x+1\right)^2+4}\ge2\\\sqrt{5\left(x+1\right)^2+9}\ge3\end{cases}}\)
\(\Rightarrow VT=\sqrt{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}\ge2+3=5\)
Và \(VP=-x^2-2x+4=-x^2-2x-1+5\)
\(=-\left(x^2+2x+1\right)+5=-\left(x+1\right)^2+5\le5\)
SUy ra \(VT\ge VP=5\Leftrightarrow x=-1\)
b)\(\sqrt{x-2\sqrt{x-1}}-\sqrt{x-1}=1\)
\(pt\Leftrightarrow\sqrt{x-1-2\sqrt{x-1}+1}-\sqrt{x-1}=1\)
\(\Leftrightarrow\left(\sqrt{x-1}-1\right)^2-\sqrt{x-1}=1\)
..... giải nốt tiếp ra x=1
c)Sửa đề \(\sqrt{x-7}+\sqrt{9-x}=x^2-16x+66\)
ĐK:....
Áp dụng BĐT Cauchy-Schwarz ta có:
\(VT^2=\left(\sqrt{x-7}+\sqrt{9-x}\right)^2\)
\(\le\left(1+1\right)\left(x-7+9-x\right)=4\)
\(\Rightarrow VT^2\le4\Rightarrow VT\le2\)
Lại có: \(VP=x^2-16x+66=x^2-16x+64+2\)
\(=\left(x-8\right)^2+2\ge2\)
Suy ra \(VT\ge VP=2\) khi \(VT=VP=2\)
\(\Rightarrow\left(x-8\right)^2+2=2\Rightarrow x-8=0\Rightarrow x=8\)

1) Ta có: \(\sqrt{21-x}+1=x\)
\(\Leftrightarrow21-x=\left(x-1\right)^2\)
\(\Leftrightarrow x^2-2x+1-21+x=0\)
\(\Leftrightarrow x^2-3x-20=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-20\right)=9+80=89\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3+\sqrt{89}}{2}\\x_2=\dfrac{3-\sqrt{89}}{2}\end{matrix}\right.\)
1)\(\sqrt{21-x}+1=x\)
\(\Leftrightarrow21-x=\left(x-1\right)^2\)
\(\Leftrightarrow21-x=x^2-2x+1\)
\(\Leftrightarrow x^2-x-20=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-4\end{matrix}\right.\)
2)\(\sqrt{8-x}+2=x\)
\(\Leftrightarrow8-x=\left(x-2\right)^2\)
\(\Leftrightarrow8-x=x^2-4x+4\)
\(\Leftrightarrow x^2-3x-4=0\Leftrightarrow\left(x-4\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-1\end{matrix}\right.\)

câu a:
\(8x^2-6x+3-2x=\left(2x-1\right)\sqrt{8x^2-6x+3}\)
đặt \(t=\sqrt{8x^2-6x+3}\Leftrightarrow t^2=8x^2-6x+3\)phương trình trở thành
\(t^2-2x=\left(2x-1\right)t\Leftrightarrow t^2-\left(2x-1\right)t-2x=0\)
có \(\Delta=\left(2x-1\right)^2+8x=\left(2x+1\right)^2\Rightarrow\orbr{\begin{cases}t=-1\\t=2x\end{cases}}\)
Câu b:
Đặt \(t=\sqrt{x^2+1}\Leftrightarrow t^2=x^2+1\left(t>0\right)\)
PT\(\Leftrightarrow t^2-\left(x+3\right)t+3x=0\)
có :\(\Delta=\left(x+3\right)^2-4.3x=\left(x-3\right)^2\Rightarrow\orbr{\begin{cases}t=3\\t=x\end{cases}}\)
ĐKXĐ: \(x\ge1\)
\(x^2+x-2+4\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)+4\sqrt{x-1}=0\)
Do \(x\ge1\Rightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x+2\right)\ge0\\\sqrt{x-1}\ge0\end{matrix}\right.\)
\(\Rightarrow\left(x-1\right)\left(x+2\right)+4\sqrt{x-1}\ge0\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\left(x-1\right)\left(x+2\right)=0\\\sqrt{x-1}=0\end{matrix}\right.\) \(\Rightarrow x=1\)
Kl:x=1