Cho tam giác ABC, biết AB<AC. M là trung điểm của BC. Tia phân giác góc A cắt BC ở D. Chứng minh D nằm giữa B và M.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 9 2021
Bài 2:
a: Xét ΔABC vuông tại A có
\(AB=BC\cdot\cos60^0\)
\(\Leftrightarrow BC=\dfrac{a}{\dfrac{1}{2}}=2a\)
\(\Leftrightarrow AC=\sqrt{BC^2-AB^2}=a\sqrt{3}\)
\(\widehat{C}=90^0-60^0=30^0\)
5 tháng 7 2021
Sửa đề: BC=29cm
Ta có: \(\dfrac{AB}{AC}=\dfrac{20}{21}\)
nên \(AB=\dfrac{20}{21}AC\)
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\left(\dfrac{20}{21}AC\right)^2+AC^2=29^2\)
\(\Leftrightarrow AC^2\cdot\dfrac{841}{441}=841\)
\(\Leftrightarrow AC^2=441\)
hay AC=21(cm)
Ta có: \(AB=\dfrac{20}{21}AC\)(cmt)
nên \(AB=\dfrac{20}{21}\cdot21=20\left(cm\right)\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=20+21+29=70\left(cm\right)\)
23 tháng 2 2016
hình vẽ của mình:
hề hề,xấu quá!
Vì 8/20=2/5 suy ra MB:AB=2/5
Vì 5/20=1/4 suy ra NC:AC=1/4
Diện tích tam giác ABN=1/4 diện tích tam giác ABC(vì có chung chiều cao hạ từ đỉnh B xuống đáy AC và có đáy NC=1/4 AC)=100x1/4=25(cm2)
Diện tích tam giác AMN=2/5 diện tích tam giác ABN(chung chiều cao hạ từ đỉnh N và có đáy BM=2/5 AB)=25x2/5=10(cm2)
đáp số:10 cm2
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2021
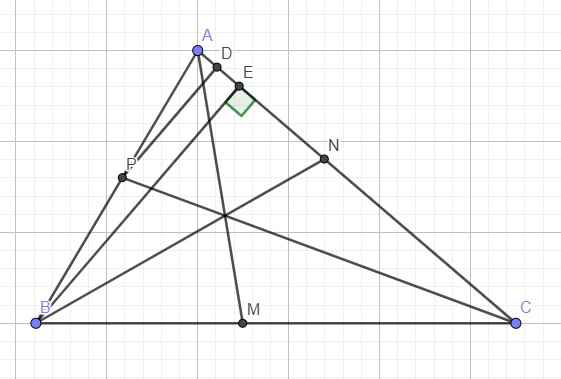
Kẻ PD và BE vuông góc AC
Định lý phân giác: \(\dfrac{AN}{NC}=\dfrac{AB}{BC}\Rightarrow\dfrac{AN}{AN+NC}=\dfrac{AB}{AB+BC}\Rightarrow\dfrac{AN}{AC}=\dfrac{AB}{AB+BC}=\dfrac{c}{a+c}\)
Tương tự: \(\dfrac{AP}{AB}=\dfrac{b}{a+b}\)
Talet: \(\dfrac{PD}{BE}=\dfrac{AP}{AB}\)
\(\dfrac{S_{APN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}PD.AN}{\dfrac{1}{2}BE.AC}=\dfrac{AP}{AB}.\dfrac{AN}{AC}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}\)
Tương tự: \(\dfrac{S_{BPM}}{S_{ABC}}=\dfrac{ac}{\left(a+b\right)\left(b+c\right)}\) ; \(\dfrac{S_{CMN}}{S_{ABC}}=\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{APN}+S_{BPM}+S_{CMN}}{S_{ABC}}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{S_{ABC}-\left(S_{APN}+S_{BPM}+S_{CMN}\right)}{S_{ABC}}=1-\left(\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\right)\)
\(=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
2. Do ABC cân tại C \(\Rightarrow AC=BC=a\)
\(\dfrac{BC}{AB}=k\Rightarrow AB=\dfrac{BC}{k}=\dfrac{a}{k}\)
Do đó:
\(\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=\dfrac{2.a.a.\dfrac{a}{k}}{2a.\left(a+\dfrac{a}{k}\right)\left(a+\dfrac{a}{k}\right)}=\dfrac{k}{\left(k+1\right)^2}\)
29 tháng 12 2019
Theo công hệ thức lương trong tam giác vuông ta có :
\(AB^2=BH.BC\Leftrightarrow9=1,8.BC\Rightarrow BC=5\left(cm\right)\)
Định lý Pytago :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
Như vậy khi ta quay tam giác ABC quanh trục AB ta thu được hình nón có đường cao \(AB=3\) , bán kính đáy \(AC=4\) và đường sinh \(BC=5\)
Diện tích xung quanh của hình nón thu được :
\(S_{xq}=\pi rl=\pi.AC.BC=20\pi\left(cm^2\right)\)
Thể tích hình nón là :
\(V=\frac{1}{3}\pi r^2h=\frac{1}{3}.\pi.4^2.3=16\pi\) ( cm khối )