f(x)= x29+x28+x27+...+x2+x+1
g(x)=x9+x2+...+x+1
CMR f(x) chia hết cho g(x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
14 tháng 7 2023
Lời giải:
Ta thấy: $x^2-3x+2=(x-1)(x-2)$. Do đó để $f(x)$ chia hết cho $g(x)$ thì $f(x)\vdots x-1$ và $f(x)\vdots x-2$
Tức là $f(1)=f(2)=0$ (theo định lý Bê-du)
$\Leftrightarrow 3-2+(a-1)+3+b=3.2^4-2.2^3+(a-1).2^2+3.2+b=0$
$\Leftrightarrow a+b=-3$ và $4a+b=-34$
$\Rightarrow a=\frac{-31}{3}$ và $b=\frac{22}{3}$
CM
3 tháng 7 2018
* Ta có:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
= x5 – (3x2 – x2) + 7x4 – 9x3 -1/4.x
= x5 – 2x2 + 7x4 – 9x3 -1/4.x
= x5 + 7x4 – 9x3 – 2x2 - 1/4
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
= 5x4 –x5+ (x2 + 3x2) – 2x3 – 1/4
= 5x4 – x5 + 4x2 – 2x3 – 1/4
= -x5 + 5x4 – 2x3 + 4x2 - 1/4
* f(x) + g(x)
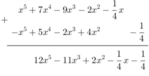
* f(x) - g(x)
28 tháng 7 2023
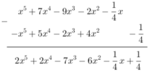
A(x)=F(x)-G(x)
=1+x+x^2+...+x^100-x^2-x^4-...-x^100
=1+x+x^3+...+x^99
Số số lẻ từ 1 đến 99 là (99-1):2+1=50(số)
A(-1)=1+(-1)+(-1)^3+...+(-1)^99
=1-50*1=1-50=-49
CM
18 tháng 12 2017
Ta có
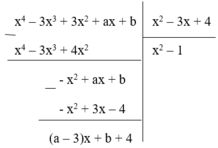
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó a - 3 = 0 b + 4 = 0
ó a = 3 b = - 4 => ab = -12
Đáp án cần chọn là: A
4 tháng 10 2023
2) Ta có đẳng thức sau: \(\left(a+b\right)\left(b+c\right)\left(c+a\right)=\left(a+b+c\right)\left(ab+bc+ca\right)-abc\)
Chứng minh thì bạn chỉ cần bung 2 vế ra là được.
\(\Rightarrow P=\left(a+b+c\right)\left(ab+bc+ca\right)-2abc\)
Do \(a+b+c⋮4\) nên ta chỉ cần chứng minh \(abc⋮2\) là xong. Thật vậy, nếu cả 3 số a, b,c đều không chia hết cho 2 thì \(a+b+c\) lẻ, vô lí vì \(a+b+c⋮4\). Do đó 1 trong 3 số a, b, c phải chia hết cho 2, suy ra \(abc⋮2\).
Do đó \(P⋮4\)
NL
1
HN
16 tháng 3 2022
Cộng vế theo vế hai phương trình, ta được: f(x)+g(x)+g(x)-f(x)=x2+1+2x \(\Leftrightarrow\) 2g(x)=x2+2x+1 \(\Leftrightarrow\) g(x)=\(\dfrac{1}{2}\)x2+x+\(\dfrac{1}{2}\).
Thế g(x) vào một trong hai phương trình, ta suy ra f(x)=\(\dfrac{1}{2}\)x2-x+\(\dfrac{1}{2}\).
15 tháng 8 2021
a: \(F\left(x\right)=x^5-3x^2+x^3-x^2-2x+5\)
\(=x^5+x^3-4x^2-2x+5\)
\(G\left(x\right)=x^5-x^4+x^2-3x+x^2+1\)
\(=x^5-x^4+2x^2-3x+1\)
b: Ta có: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^5+x^3-4x^2-2x+5+x^5-x^4+2x^2-3x+1\)
\(=2x^5-x^4+x^3-2x^2-5x+6\)
Lời giải:
\(f(x)=1+x+x^2+x^3+...+x^{27}+x^{28}+x^{29}\)
\(=(1+x+x^2+x^3+...+x^9)+(x^{10}+x^{11}+...+x^{19})+(x^{20}+x^{21}+...+x^{29})\)
\(=(1+x+x^2+...+x^9)+x^{10}(1+x+x^2+...+x^9)+x^{20}(1+x+x^2+...+x^9)\)
\(=(1+x+x^2+..+x^9)(1+x^{10}+x^{20})=g(x)(1+x^{10}+x^{20})\)
Suy ra $f(x)$ chia hết cho $g(x)$
Ta có đpcm.