Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: góc B=90-60=30 độ
Xét ΔABC có góc C<góc B<góc A
nên AB<AC<BC
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
c: ΔBAE=ΔBHE
=>EA=EH
=>ΔEAH cân tại E
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
góc ABE=góc hBE
=>ΔABE=ΔHBE
c: Xét ΔBHM vuông tại H và ΔBAC vuông tại A có
BH=BA
góc HBM chung
=>ΔBHM=ΔBAC
=>BM=BC
=>ΔBMC cân tại B
mà BN là đường phân giác
nên N là trung điểm của CM
=>NM=NC
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: Xét ΔEBC có góc EBC=góc ECB
nên ΔEBC cân tại E
mà EH là đường cao
nên H là trung điểm của BC
=>HB=HC
d: Xét ΔEAI vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEI=góc HEC
=>ΔEAI=ΔEHC
=>EI=EC>EH
a) Xét \(\Delta ABE\) và \(\Delta HBE\):
BE chung
\(\widehat{ABE}=\widehat{EBH}\)
\(\widehat{EAB}=\widehat{EHB}=90^o\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) \(\widehat{EBH}=\dfrac{1}{2}\widehat{B}=30^o\)
\(\widehat{ACB}=90^o-\widehat{B}=30^o\)
\(\Rightarrow\Delta EBC\) cân tại E
Mà EH vuông góc BC
\(\Rightarrow HB=HC\)
c) \(\widehat{HEB}=90^o-\widehat{EBH}=60^o\)
\(KH//BE\Rightarrow\widehat{KHE}=\widehat{HEB}=60^o\)
\(\widehat{HEB}+\widehat{AEB}=60^o+60^o=120^o\)
\(\Rightarrow\widehat{KEH}=180^o-120^o=60^o\)
\(\Rightarrow\Delta EHK\) đều
d) Theo phần a. \(\Delta ABE=\Delta HBE\Rightarrow AE=EH\)
\(\Delta IAE\) vuông ở A \(\Rightarrow IE>AE\)
\(\Rightarrow IE>EH\)
a) Xét ΔABEΔABE và ΔHBEΔHBE:
BE chung
ˆABE=ˆEBHABE^=EBH^
ˆEAB=ˆEHB=90oEAB^=EHB^=90o
⇒ΔABE=ΔHBE(ch−gn)⇒ΔABE=ΔHBE(ch−gn)
b) ˆEBH=12ˆB=30oEBH^=12B^=30o
ˆACB=90o−ˆB=30oACB^=90o−B^=30o
⇒ΔEBC⇒ΔEBC cân tại E
Mà EH vuông góc BC
⇒HB=HC⇒HB=HC
c) ˆHEB=90o−ˆEBH=60oHEB^=90o−EBH^=60o
KH//BE⇒ˆKHE=ˆHEB=60oKH//BE⇒KHE^=HEB^=60o
ˆHEB+ˆAEB=60o+60o=120oHEB^+AEB^=60o+60o=120o
⇒ˆKEH=180o−120o=60o⇒KEH^=180o−120o=60o
⇒ΔEHK⇒ΔEHK đều
d) Theo phần a. ΔABE=ΔHBE⇒AE=EHΔABE=ΔHBE⇒AE=EH
ΔIAEΔIAE vuông ở A ⇒IE>AE
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔABE=ΔHBE
b: góc HEC+góc AEH=180 độ
góc AEH+góc ABH=180 độ
=>góc HEC=góc ABH=2*góc ABE
c: AE=EH
EH<EC
=>AE<EC
a) xét ΔΔvuông ABE vàΔΔvuông HBE có:
BE là cạnh chung
gcABE=gcHBE(BE là tia p.g của gc ABC)
=> tg ABE=tgHBE(cạnh huyền góc nhọn)
b) theo câu a: tg ABE= tg HBE (cmt)=>AB=BH (1)
trong tg vuông ABC có: gc B =60o=> gc C=30o
=> AB=1212 BC(2)
=> BH = BC2BC2mà H thuộc BC => H là trung điểm BC
xét tg BCE có:H là TĐ của BC(cmt)
HK//BE(gt)=> K là trung điểm EC
xét tg vuông HEC có: HK là đường trung tuyến ứng vs cạnh huyền
=> HK=EK= EC2EC2=> tg HEK cân ở K
lại có:gc EKH = gc ACB+gc KHC( góc ngoài cuả tgHKC)
gc KHC=gc EBC=30o( đồng vị ,HK//BE)
do đó gc EHK=gc ACB+gc EBC=30+30=60o
tam giác cân có 1 góc = 60 o là tam giác đều
c)(nhiều cách lúm)
trong tg vuông HBM: gc HBM= 60o=>gc HMB= 30o
=>BH=12BMBH=12BMmà BH= 12BC12BC(cmt )
=> BM=BC=> tg BMC cân ở B
BN là đường p.g của gcMBC
=> BN đồng thời là đường trung trực của tgMBC hay của cạnh MC
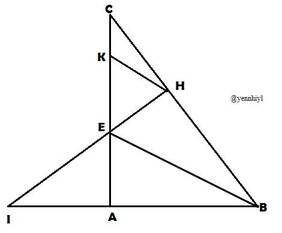
Đề sai chỗ kia nha "Tia phân giác góc B cắt BC(AC nha) tại E"
Hình tự vẽ nha, thanks
a) Trong tam giác ABC vuông tại A có:
\(\widehat{ABC}=\widehat{A}-\widehat{C}=90^o-30^o=60^o\)
Mà \(\widehat{C}=30^o\)
\(\widehat{A}=90^o\)
Do đó: BC>AC>AB (do cái gì đó, lên lớp 8 quên mất rồi)
b)Xét 2 tam giác vuông: \(\Delta ABE\) và \(\Delta HBE\), có:
cạnh huyền: BE: chung
góc nhọn: \(\widehat{ABE}=\widehat{HBE}\) (BE là tia phân giác của góc B)
Do đó: \(\Delta ABE=\Delta HBE\)(c/h-g/n)
c)Do \(\Delta ABE=\Delta HBE\left(cmt\right)\Rightarrow AE=HE\)(2 cạnh tương ứng)
\(\Rightarrow\Delta EAH\) cân tại E
d) Ta có: HK//BE \(\Rightarrow\widehat{CHK}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^o}{2}=30^o\)
Lại có: \(\widehat{C}=30^o\)
Do đó: \(\Delta KHC\) cân tại K
\(\Rightarrow KC=KH\)(2 cạnh tương ứng)
Ta cũng có: \(\widehat{KHE}=\widehat{CHE}-\widehat{CHK}=60^o-30^o=30^o\)
Xét tam giác vuông CHE, có:
\(\widehat{CEH}=90^o-\widehat{C}=90^o-30^o=60^o\)
Xét \(\Delta EHK\), có:
\(\widehat{KHE}=\widehat{KEH}=60^o\)
\(\Rightarrow\Delta KHE\) là tam giác đều
\(\Rightarrow HE=EK=KH\)
Mà AE=HE (cmt) và KC=KH(cmt)
Do đó: AE=EK=KC(đpcm)