khi nào 2 thẻ vàng thành 1 thẻ đỏ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
+ Nếu các thẻ vàng nằm ở vị trí lẻ thì các thẻ đỏ nằm ở vị trí chẵn
ta có. 7!.7! cách xếp khác nhau
+ Nếu các thẻ vàng nằm ở vị trí chẵn thì các thẻ đỏ nằm ở vị trí lẻ
ta có. 7!.7! cách xếp khác nhau
Vậy có tất cả
![]()

Đáp án D
+ Nếu các thẻ vàng nằm ở vị trí lẻ thì các thẻ đỏ nằm ở vị trí chẵn
ta có. 7!.7! cách xếp khác nhau
+ Nếu các thẻ vàng nằm ở vị trí chẵn thì các thẻ đỏ nằm ở vị trí lẻ
ta có. 7!.7! cách xếp khác nhau
Vậy có tất cả:
7!.7!+7!.7! = 50803200 cách

+ Nếu các thẻ vàng nằm ở vị trí lẻ thì các thẻ đỏ nằm ở vị trí chẵn, ta có. 7!.7! cách xếp khác nhau
+ Nếu các thẻ vàng nằm ở vị trí chẵn thì các thẻ đỏ nằm ở vị trí lẻ, ta có. 7!.7! cách xếp khác nhau
Vậy có tất cả 7! . 7! + 7! . 7! = 50803200 cách
Đáp án cần chọn là D

a) Các kết quả có thể xảy ra trong 2 lần lấy tấm thẻ từ 2 hộp được thể hiện ở sơ đồ hình cây như hình dưới đây:
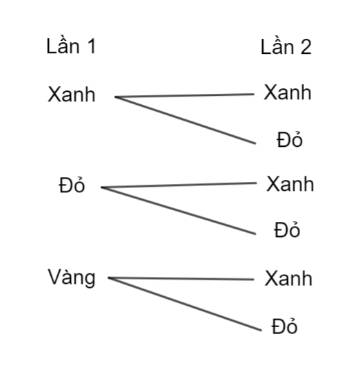
b)
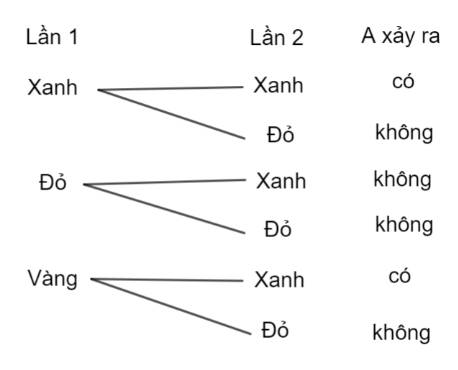
Gọi A là biến cố “Trong 2 thẻ lấy ra không có thẻ màu đỏ nào” là biến cố đối của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”
Dựa vào sơ đồ hình cây ta thấy có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho I. Do đó: \(P(A) = \frac{2}{6} = \frac{1}{3}\)
Vậy xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ” là \(1 - \frac{1}{3} = \frac{2}{3}\)

a) Kí hiệu \({X_1},{X_2},...,{X_7}\) là bảy thẻ màu xanh, \({D_1},{D_2},...,{D_5}\) là 5 thẻ màu đỏ và \({V_1},{V_2}\) là hai thẻ màu vàng.
Ta có không gian mẫu là \(\Omega = \left\{ {{X_1},{X_2},...,{X_7},{D_1},{D_2},...,{D_5},{V_1},{V_2}} \right\}\).
b) Ta có \(A = \left\{ {{D_1},{D_2},{D_3},{D_4},{D_5},{V_1},{V_2}} \right\},B = \left\{ {{X_2},{X_3},{D_2},{D_3},{V_2}} \right\}\).


a. Không gian mẫu gồm 10 phần tử:
Ω = {1, 2, 3, …, 10}
b. A, B, C "là các biến cố".
+ A: "Lấy được thẻ màu đỏ"
⇒ A = {1, 2, 3, 4, 5}
+ B: "Lấy được thẻ màu trắng"
⇒ B = {7, 8, 9, 10}
+ C: "Lấy được thẻ ghi số chắn".
⇒ C = {2, 4, 6, 8, 10}

Khi đá bóng
khi trong đá bóng cầu thủ chơi bẩn