Giải phương trình: -2sin3x-6cos3x+cosx+3sinx=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
Nguyễn Đức Trí
VIP
9 tháng 10 2023
\(sin2x-cos2x+3sinx-cosx-1=0\)
\(\Leftrightarrow2sinxcosx-\left(1-2sin^2x\right)+3sinx-cosx-1=0\)
\(\Leftrightarrow2sinxcosx-1+2sin^2x+3sinx-cosx-1=0\)
\(\Leftrightarrow2sin^2x+3sinx-2+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow2\left(sinx-\dfrac{1}{2}\right)\left(sinx+2\right)+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+2\right)+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+2+cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2sinx-1=0\\sinx+cosx+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx+cosx=-2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}sinx=sin\dfrac{\pi}{6}\\\sqrt[]{2}\left(sinx.\dfrac{1}{\sqrt[]{2}}+cosx.\dfrac{1}{\sqrt[]{2}}\right)=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\\\sqrt[]{2}sin\left(x+\dfrac{\pi}{4}\right)=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\\sin\left(x+\dfrac{\pi}{4}\right)=-\sqrt[]{2}\left(vô.lý\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
NJ
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
Đặt \(tan\dfrac{x}{2}=t\) ta được:
\(\dfrac{6t}{1+t^2}+\dfrac{1-t^2}{1+t^2}-4t+1=0\)
\(\Leftrightarrow-2t^3+t+1=0\)
\(\Leftrightarrow\left(t-1\right)\left(2t^2+2t+1\right)=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow tan\dfrac{x}{2}=1\)
\(\Rightarrow\dfrac{x}{2}=\dfrac{\pi}{4}+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
\(\Leftrightarrow\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=sin3x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{3}\right)=sin3x\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=x+\dfrac{\pi}{3}+k2\pi\\3x=\dfrac{2\pi}{3}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
16 tháng 8 2021
a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
16 tháng 8 2021
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)
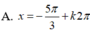
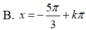
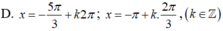
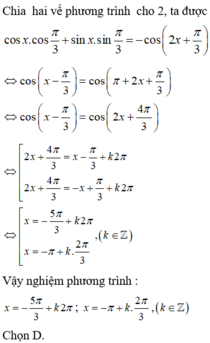
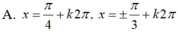
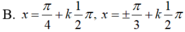
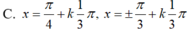
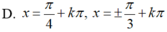
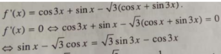
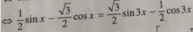
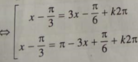
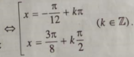
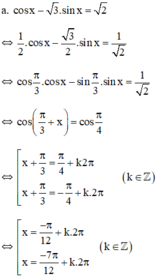
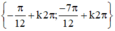(k ∈ Z)
TH1 cosx=0 \(\Leftrightarrow1=0\left(vl\right)\)
TH2 \(cosx\ne0\) chia 2 vế cho \(cos^3x\)
\(\Leftrightarrow-2tan^3x-6+1+tân^2x+3tanx\left(1+tan^2x\right)=0\)
\(\Leftrightarrow tan^3x+tan^2x+3tanx-5=0\)
\(\Leftrightarrow\left(tanx-1\right)\left(tan^2x+2tanx+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tan^2x+2tanx+5=0\left(VN\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\left(k\in Z\right)\)