Câu 1: Tính
a. \(\sqrt{3\dfrac{6}{25}}\) b. \(\sqrt[3]{261}\) c. \(\sqrt{8,1}\) . \(\sqrt{20}\). \(\sqrt{8}\)
d. \(\sqrt{11+2\sqrt{30}}-\sqrt{11-2\sqrt{30}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
8 tháng 7 2023
\(a,\dfrac{3}{5}-\dfrac{1}{2}\sqrt{1\dfrac{11}{25}}=\dfrac{3}{5}-\dfrac{1}{2}\sqrt{\dfrac{36}{25}}=\dfrac{3}{5}-\dfrac{1}{2}.\dfrac{\sqrt{6^2}}{\sqrt{5^2}}=\dfrac{3}{5}-\dfrac{1}{2}.\dfrac{6}{5}=\dfrac{3}{5}-\dfrac{6}{10}=\dfrac{3}{5}-\dfrac{3}{5}=0\)
\(b,\left(5+2\sqrt{6}\right)\left(5-2\sqrt{6}\right)=5^2-\left(2\sqrt{6}\right)^2=25-2^2.\sqrt{6^2}=25-4.6=25-24=1\)
\(c,\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{4-2\sqrt{3}}\\ =\left|2-\sqrt{3}\right|+\sqrt{\sqrt{3^2}-2\sqrt{3}+1}\\ =2-\sqrt{3}+\sqrt{\left(\sqrt{3}-1\right)^2}\\ =2-\sqrt{3}+\left|\sqrt{3}-1\right|\\ =2-\sqrt{3}+\sqrt{3}-1\\ =1\)
\(d,\dfrac{\left(x\sqrt{y}+y\sqrt{x}\right)\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{xy}}\left(dk:x,y>0\right)\\ =\dfrac{\left(\sqrt{x^2}.\sqrt{y}+\sqrt{y^2}.\sqrt{x}\right)\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{xy}}\\ =\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{xy}}\\ =\sqrt{x^2}-\sqrt{y^2}\\ =\left|x\right|-\left|y\right|\\ =x-y\)
30 tháng 9 2021
a: Ta có: \(A=\left(\dfrac{6+\sqrt{20}}{3+\sqrt{5}}+\dfrac{\sqrt{14}-\sqrt{2}}{\sqrt{7}-1}\right):\left(2+\sqrt{2}\right)\)
\(=\left(2+\sqrt{2}\right):\left(2+\sqrt{2}\right)\)
=1
b: Ta có: \(B=\sqrt{5-2\sqrt{6}}+\sqrt{5+2\sqrt{6}}-\dfrac{11}{2\sqrt{3}+1}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{3}+\sqrt{2}-2\sqrt{3}+1\)
=1
27 tháng 5 2021
\(\sqrt{15-\sqrt{216}}+\sqrt{33-12\sqrt{6}}=\sqrt{6-6\sqrt{6}+9}+\sqrt{24-12\sqrt{6}+9}=\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(\sqrt{24}-3\right)^2}=\left|3-\sqrt{6}\right|+\left|\sqrt{24}-3\right|=3-\sqrt{6}+\sqrt{24}-3=2\sqrt{6}-\sqrt{6}=\sqrt{6}\)
27 tháng 5 2021
\(\dfrac{2\sqrt{8}-\sqrt{12}}{\sqrt{18}-\sqrt{48}}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{30}+\sqrt{162}}=-\dfrac{\sqrt{2}\left(\sqrt{6}-4\right)}{\sqrt{3}\left(\sqrt{6}-4\right)}-\dfrac{\sqrt{5}+\sqrt{27}}{\sqrt{6}\left(\sqrt{5}+\sqrt{27}\right)}=\dfrac{-\sqrt{2}}{\sqrt{3}}-\dfrac{1}{\sqrt{6}}=\dfrac{-\sqrt{6}}{3}-\dfrac{\sqrt{6}}{6}=-\dfrac{\sqrt{6}}{2}\).
RK
23 tháng 6 2021
a) \(\sqrt{\dfrac{1}{8}}\cdot\sqrt{2}\cdot\sqrt{125}\cdot\sqrt{\dfrac{1}{5}}\) = \(\sqrt{\dfrac{1}{8}\cdot2}.\sqrt{125\cdot\dfrac{1}{5}}=\sqrt{\dfrac{1}{4}}.\sqrt{25}=\dfrac{1}{2}\cdot5=2,5\)
RK
23 tháng 6 2021
b)\(\sqrt{\sqrt{2}-1}.\sqrt{\sqrt{2}+1}=\sqrt{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}=\sqrt{2-1}=1\)
HP
3 tháng 9 2021
b, \(\dfrac{2}{\sqrt{5}+2}+\dfrac{2}{2-\sqrt{5}}\)
\(=\dfrac{2\left(\sqrt{5}-2\right)}{5-4}-\dfrac{2\left(\sqrt{5}+2\right)}{5-4}\)
\(=2\sqrt{5}-4-2\sqrt{5}-4=-8\)
24 tháng 8 2021
a)\(2\sqrt{\dfrac{16}{3}}-3\sqrt{\dfrac{1}{27}}-6\sqrt{\dfrac{4}{75}}\)
\(=2.\sqrt{\dfrac{4^2}{3}}-3.\sqrt{\dfrac{1}{3.3^2}}-6\sqrt{\dfrac{2^2}{3.5^2}}\)
\(=2.\dfrac{4}{\sqrt{3}}-3.\dfrac{1}{3\sqrt{3}}-6.\dfrac{2}{5\sqrt{3}}=\dfrac{8}{\sqrt{3}}-\dfrac{1}{\sqrt{3}}-\dfrac{12}{5\sqrt{3}}\)\(=\dfrac{23}{5\sqrt{3}}=\dfrac{23\sqrt{3}}{15}\)
b)\(\left(6\sqrt{\dfrac{8}{9}}-5\sqrt{\dfrac{32}{25}}+14\sqrt{\dfrac{18}{49}}\right).\sqrt{\dfrac{1}{2}}\)
\(=6\sqrt{\dfrac{8}{9}.\dfrac{1}{2}}-5\sqrt{\dfrac{32}{25}.\dfrac{1}{2}}+14\sqrt{\dfrac{18}{49}.\dfrac{1}{2}}\)
\(=6\sqrt{\dfrac{4}{9}}-5\sqrt{\dfrac{16}{25}}+14\sqrt{\dfrac{9}{49}}\)\(=6.\dfrac{2}{3}-5.\dfrac{4}{5}+14.\dfrac{3}{7}=6\)
c)\(\sqrt{\left(\sqrt{2}-2\right)^2}-\sqrt{6+4\sqrt{2}}=\left|\sqrt{2}-2\right|-\sqrt{4+2.2\sqrt{2}+2}=2-\sqrt{2}-\sqrt{\left(2+\sqrt{2}\right)^2}\)
\(=2-\sqrt{2}-\left(2+\sqrt{2}\right)=-2\sqrt{2}\)
21 tháng 12 2023
Bài 1:
a: \(5\sqrt{8}-4\sqrt{27}-2\sqrt{75}+\sqrt{108}\)
\(=5\cdot2\sqrt{2}-4\cdot3\sqrt{3}-2\cdot5\sqrt{3}+6\sqrt{3}\)
\(=10\sqrt{2}-12\sqrt{3}-10\sqrt{3}+6\sqrt{3}\)
\(=10\sqrt{2}-16\sqrt{3}\)
b: \(\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(1-\sqrt{6}\right)^2}\)
\(=\left|3-\sqrt{6}\right|+\left|1-\sqrt{6}\right|\)
\(=3-\sqrt{6}+\sqrt{6}-1\)
=3-1=2
c: \(\dfrac{5\sqrt{3}-3\sqrt{5}}{\sqrt{5}-\sqrt{3}}+\dfrac{1}{4+\sqrt{15}}\)
\(=\dfrac{\sqrt{15}\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{5}-\sqrt{3}}+\dfrac{1\left(4-\sqrt{15}\right)}{16-15}\)
\(=\sqrt{15}+4-\sqrt{15}=4\)
d: \(\dfrac{2\sqrt{3-\sqrt{5}}\cdot\left(3+\sqrt{5}\right)}{\sqrt{10}-\sqrt{2}}-\dfrac{\sqrt{15}+\sqrt{5}}{\sqrt{12}+2}\)
\(=\dfrac{\sqrt{3-\sqrt{5}}\cdot\sqrt{2}\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}\left(\sqrt{3}+1\right)}{2\left(\sqrt{3}+1\right)}\)
\(=\dfrac{\sqrt{6-2\sqrt{5}}\cdot\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}}{2}\)
\(=\sqrt{\left(\sqrt{5}-1\right)^2}\cdot\dfrac{\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}}{2}\)
\(=3+\sqrt{5}-\dfrac{\sqrt{5}}{2}=3+\dfrac{\sqrt{5}}{2}\)
Bài 2:
Vẽ đồ thị:
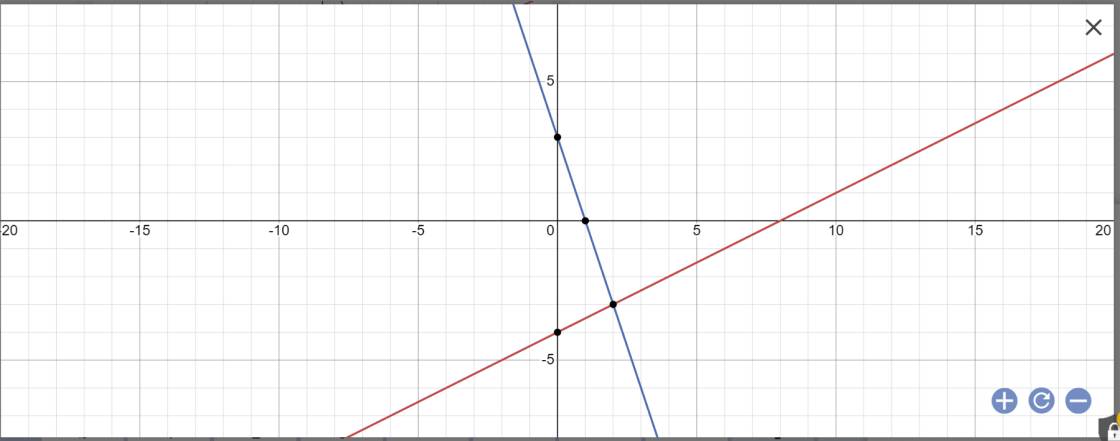
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x-4=-3x+3\)
=>\(\dfrac{1}{2}x+3x=3+4\)
=>\(\dfrac{7}{2}x=7\)
=>x=2
Thay x=2 vào y=-3x+3, ta được:
\(y=-3\cdot2+3=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)
\(a,=\sqrt{\dfrac{81}{25}}=\dfrac{9}{5}\\ b,\approx6,39\\ c,=\sqrt{8,1\cdot20\cdot8}=\sqrt{81\cdot16}=\sqrt{81}\cdot\sqrt{16}=9\cdot4=36\\ d,=\sqrt{\left(\sqrt{6}+\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{6}-\sqrt{5}\right)^2}\\ =\sqrt{6}+\sqrt{5}-\sqrt{6}+\sqrt{5}=2\sqrt{5}\)
a) \(\sqrt{3\dfrac{6}{25}}=\sqrt{\dfrac{81}{25}}=\dfrac{9}{5}\)
b) \(\sqrt[3]{216}=6\)
c) \(\sqrt{8,1}.\sqrt{20}.\sqrt{8}=\dfrac{9\sqrt{10}}{10}.2\sqrt{5}.2\sqrt{2}=36\)
d) \(\sqrt{11+2\sqrt{30}}-\sqrt{11-2\sqrt{30}}=\sqrt{\left(\sqrt{6}+\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{6}-\sqrt{5}\right)^2}=\sqrt{6}+\sqrt{5}-\sqrt{6}+\sqrt{5}=2\sqrt{5}\)