Ai giúp em câu b,c với ạ e cảm ơn !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(26,\\ a,\sin45^0=\cos45^0< \sin50^025'< \sin57^048'=\cos32^012'< \sin72^0=\cos18^0< \sin75^0\\ b,\tan37^026'< \tan47^0< \tan58^0=\cot32^0< \tan63^0< \tan66^019'=\cot23^041'\\ 27,\\ A=\dfrac{\left(\sin^226^0+\sin^264^0\right)+2\left(\cos^215^0+\cos^275^0\right)}{\left(\sin^255^0+\cos^255^0\right)+\left(\sin^242^0+\cos^242^0\right)}-\dfrac{\tan81^0}{2\tan81^0}\\ A=\dfrac{\left(\sin^226^0+\cos^226^0\right)+2\left(\sin^215^0+\cos^215^0\right)}{1+1}-\dfrac{1}{2}\\ A=\dfrac{1+2}{2}-\dfrac{1}{2}=2-\dfrac{1}{2}=\dfrac{3}{2}\)
\(28,\\ \sin^2\alpha=1-\cos^2\alpha=1-\dfrac{1}{2}=\dfrac{1}{2}\\ \Leftrightarrow\sin\alpha=\dfrac{\sqrt{2}}{2}\)

Bài 2 : (1) liên kết ; (2) electron ; (3) liên kết ; (4) : electron ; (5) sắp xếp electron
Bài 4 :
$\dfrac{M_X}{4} = \dfrac{M_K}{3} \Rightarrow M_X = 52$
Vậy X là crom,KHHH : Cr
Bài 5 :
$M_X = 3,5M_O = 3,5.16 = 56$ đvC
Tên : Sắt
KHHH : Fe
Bài 9 :
$M_Z = \dfrac{5,312.10^{-23}}{1,66.10^{-24}} = 32(đvC)$
Vậy Z là lưu huỳnh, KHHH : S
Bài 10 :
a) $PTK = 22M_{H_2} = 22.2 = 44(đvC)$
b) $M_{hợp\ chất} = X + 16.2 = 44 \Rightarrow X = 12$
Vậy X là cacbon, KHHH : C
Bài 11 :
a) $PTK = 32.5 = 160(đvC)$
b) $M_{hợp\ chất} = 2A + 16.3 = 160 \Rightarrow A = 56$
Vậy A là sắt
c) $\%Fe = \dfrac{56.2}{160}.100\% = 70\%$

Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{2022^2}< \dfrac{1}{2021.2022}\)
cộng vế với vế
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2022^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}=\dfrac{2021}{2022}\)
Vậy ta có đpcm

\(\dfrac{x+4}{3}=\dfrac{x-11}{-6}\)
\(\dfrac{2x+8}{6}=\dfrac{-x+11}{6}\)
\(\Leftrightarrow2x+8=-x+11\)
\(\Leftrightarrow3x=3\)
\(\Leftrightarrow x=1\)


a: Thay x=16 vào B, ta được:
B=4+1=5
b: \(A=\dfrac{x+\sqrt{x}+10-\sqrt{x}-3}{x-9}\cdot\left(\sqrt{x}-3\right)=\dfrac{x+7}{\sqrt{x}+3}\)
c: Để A<B thì \(x+7< x+4\sqrt{x}+3\)
=>x>1



Bài 3:
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)

\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)


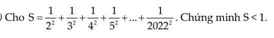
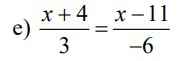
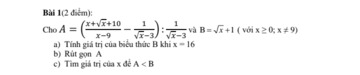


 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.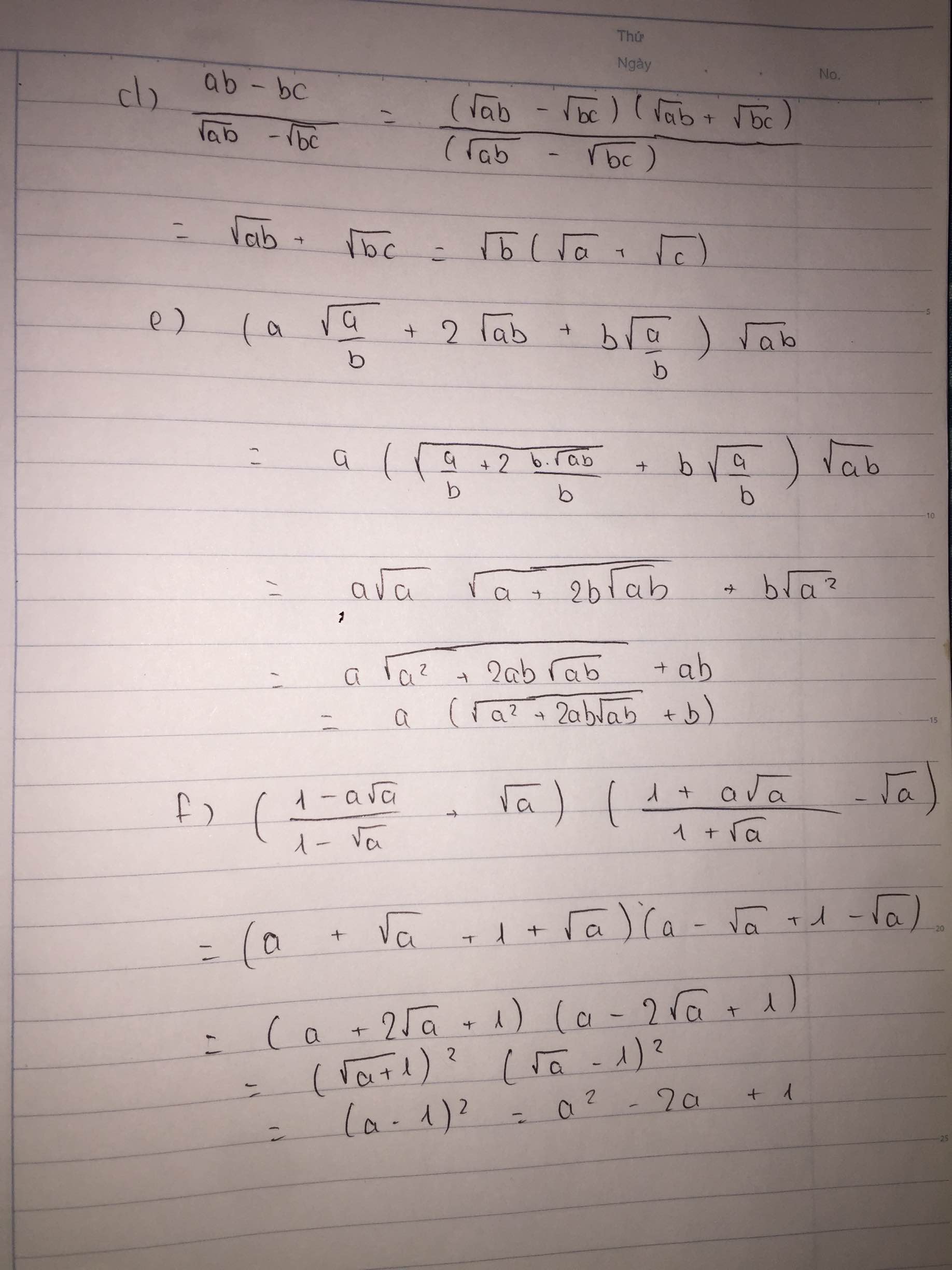
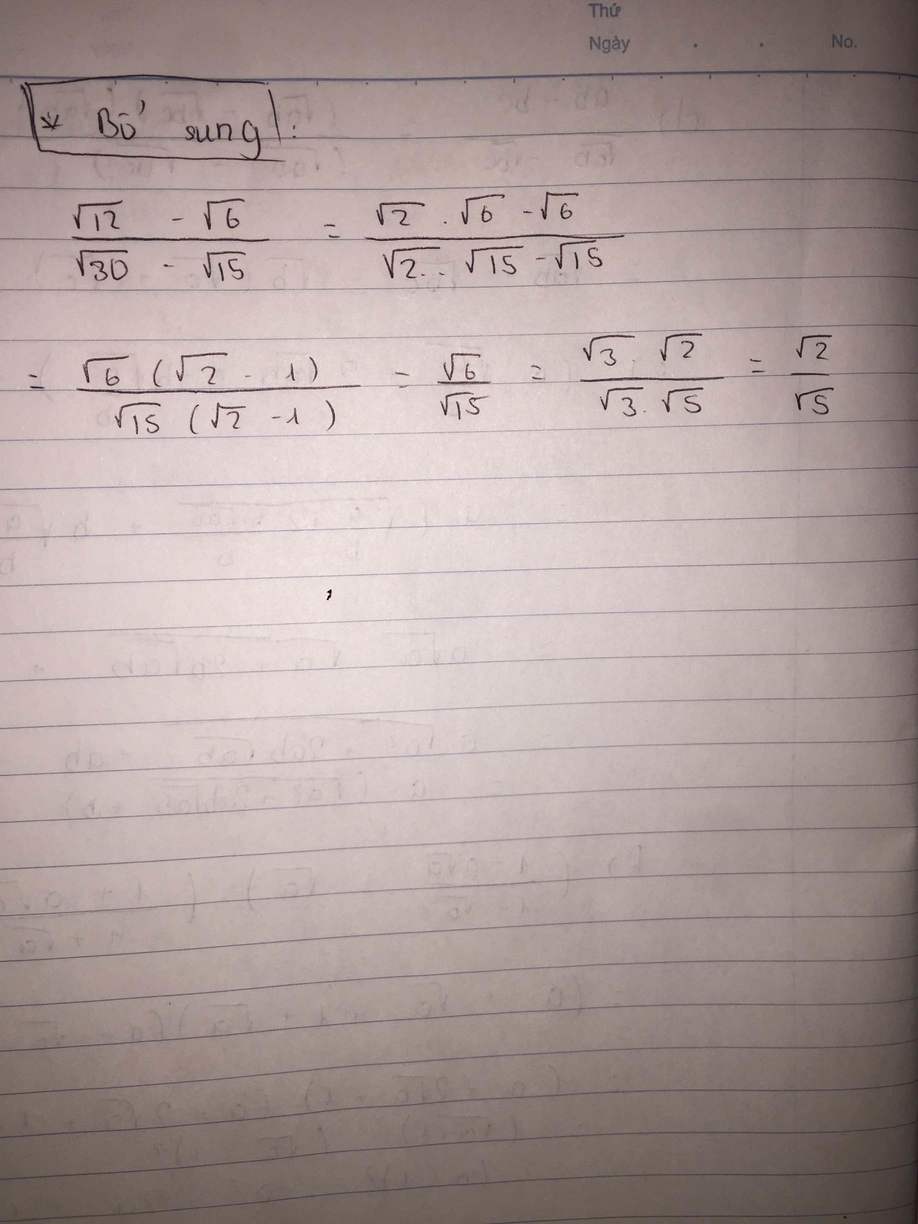
b) \(4x^2\left(x-y\right)+y^4\left(y-x\right)=4x^2\left(x-y\right)-y^4\left(x-y\right)=\left(x-y\right)\left(4x^2-y^4\right)\)
c) \(2a-b-4a^2+4ab-b^2=2a-b-\left(4a^2-4ab+b^2\right)=2a-b-\left[\left(2a\right)^2-2\cdot2ab+b^2\right]\)
\(=\left(2a-b\right)-\left(2a-b\right)^2=\left(2a-b\right)\left(1-2a+b\right)\)