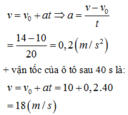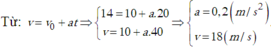Câu 7. Một xe ô tô đang chuyển động thẳng qua điểm A với vận tốc 10 m/s thì tăng tốc, chuyển động nhanh dần đều và đến điểm B thì đạt vận tốc 20 m/s. Gọi C là trung điểm của AB. Tìm vận tốc của xe khi đi qua C.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KA
2 tháng 1
Chọn hệ quy chiếu với gốc tọa độ và gốc thời gian là nơi và lúc ô tô bắt đầu tăng tốc. Chiều dương là chiều chuyển động
Gia tốc của ô tô là:
`a = (v-v_0)/(\Deltat) = (20-15)/10 = 0,5 (m//s)`
Quãng đường ô tô đi được là:
`s = v_0 \Deltat + 1/2 a (\Deltat)^2 = 15.10 + 1/2 . 0,5 . 10^2 = 175(m)`.
VT
22 tháng 6 2018
Chọn đáp án C
− Gia tốc của xe: a = v − v 0 Δ t = 0,5 m/s
− Vận tốc sau 40 s kể từ khi tăng tốc: v = v 0 + a t = 30 m / s
5 tháng 10 2021
a) Gia tốc a: \(v=v_0+at\Rightarrow a=\dfrac{v-v_0}{t}=\dfrac{14-10}{20}=0,2\)m/s2
Quãng đường ôto đi được trong20s:
\(S=v_0t+\dfrac{1}{2}at^2=10\cdot20+\dfrac{1}{2}\cdot0,2\cdot20^2=240m\)
b) Vận tốc ôt sau 25s tăng ga:
\(v'=v_0+at=10+0,2\cdot25=15\)m/s
c) Quãng đường ôto đi được sau 30s:
\(S_{30}=v_0t+\dfrac{1}{2}at^2=10\cdot30+\dfrac{1}{2}\cdot0,2\cdot30^2=390m\)
Quãng đường ôto đi được sau 29s:
\(S_{29}=v_0t+\dfrac{1}{2}at^2=10\cdot29+\dfrac{1}{2}\cdot0,2\cdot29^2=374,1m\)
Quãng đường vật đi trong giây thứ 30:
\(S=390-374,1=15,9m\)
5 tháng 10 2021
\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{v-vo}{t}=\dfrac{14-10}{20}=0,2m/s^2\Rightarrow S\left(20s\right)=vot+\dfrac{1}{2}at^2=240m\\v'=vo+at'=10+0,2.25=15m/s\\S\left(30s\right)=vot''+\dfrac{1}{2}at''^2=10.30+\dfrac{1}{2}.0,2.30^2=390m\\S\left(giây30\right)=S\left(30s\right)-S\left(29s\right)=390-374,1=15,9m\end{matrix}\right.\)
18 tháng 12 2021
Gia tốc vật: \(v=v_0+at\)
\(\Rightarrow a=\dfrac{v-v_0}{t}=\dfrac{15-5}{20}=0,5\)m/s2
Quãng đường xe sau 20s tăng ga:
\(S=v_0t+\dfrac{1}{2}at^2=5\cdot20+\dfrac{1}{2}\cdot0,5\cdot20^2=200m\)
VT
19 tháng 8 2018
Giải:
Áp dụng công thức v 1 = v 0 + a t ⇒ a = v 1 − v 0 t = 20 − 15 10 = 0 , 5 ( m / s 2 )
Vận tốc của ô tô sau khi đi được 20s v 2 = v 0 + a t 2 ⇒ v 2 = 15 + 0 , 5.20 = 25 m / s