Số học sinh giỏi của ba lớp 7A0, 7A1, 7A2 tỉ lệ với 3;5;7. Hỏi số học sinh giỏi của mỗi lớp, biết số học sinh giỏi của lớp 7A0 nhiều hơn số học sinh giỏi của lớp 7A2 là 12 học sinh.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 11 2021
Gọi lớp 7a1,7a2,7a3 lần lượt là a,b,c và a+b+c=105
theo t/c dãy tỉ số bằng nhau ta có:
\(\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{a+b+c}{4+5+6}=\frac{105}{15}=7\)
\(\hept{\begin{cases}\frac{a}{4}=7\Rightarrow a=7.4=28\\\frac{b}{5}=7\Rightarrow b=7.5=35\\c=105-\left(28+35\right)=42\end{cases}}\)
Vậy 7a1 có 28 hs
7a2 có 35hs
7a3 có 42hs
20 tháng 8 2021
Lớp 7a1 có số HS là:
5:(9-8)x8=40(HS)
Lớp 7a2 có số học sinh là:
40+5=45(HS)
ĐS: lớp 7a1:40 học sinh
lớp 7a2:45 học sinh
7 tháng 12 2016
Gọi số học sinh 2 lớp 7A1 và 7A2 lần lượt là: a, b ( a, b thuộc N* )
Theo đề bài, ta có:
\(\frac{a}{8}=\frac{b}{9}\) và b - a = 5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{8}=\frac{b}{9}=\frac{b-a}{9-8}=\frac{5}{1}=5\)
Do đó \(\frac{a}{8}=5=>a=5\cdot8=40\)
\(\frac{b}{9}=5=>b=5\cdot9=45\)
Vậy số học sinh 2 lớp 7A1 và 7A2 lần lượt là: 40, 45 ( học sinh )
7 tháng 12 2016
Gọi số học sinh 2 lớp 7A1 và lớp 7A2 lần lượt là a,b (a,b\(\in\)N*;b>a>5)
Theo đề bài ta có:
Lớp 7A1 ít hơn lớp 7A2 là 5 học sinh suy ra \(b-a=5\)
Tỉ số học sinh của hai lớp 7A1 và 7A2 là 8:9 suy ra \(a:b=8:9\Rightarrow\frac{a}{8}=\frac{b}{9}\)
Áp dụng tc dãy tỉ số bằng nhau ta có:
\(\frac{a}{8}=\frac{b}{9}=\frac{b-a}{9-8}=\frac{5}{1}=5\)
\(\Rightarrow\begin{cases}\frac{a}{8}=5\Rightarrow a=5\cdot8=40\\\frac{b}{9}=5\Rightarrow b=5\cdot9=45\end{cases}\)(thỏa mãn)
Vậy số học sinh 2 lớp 7A1 và lớp 7A2 lần lượt là 40 em; 45 em
WJ
28 tháng 10 2015
Gọi số HS 3 lớp lần lượt là x,y,z
Ta có: \(\frac{x}{7}=\frac{y}{9}=\frac{z}{8}=\frac{x+y+z}{7+9+8}=\frac{120}{24}=5\)
\(\Rightarrow\frac{x}{7}=5\Rightarrow x=35;\frac{x}{9}=5\Rightarrow x=45;\frac{z}{8}=5\Rightarrow z=40\)
Vậy số HS lớp 7A1 là 35 (hs), lớp 7A2 là 45 (hs), lớp 7A3 là 40 (hs)
CM
17 tháng 11 2018
Gọi x,y,z,t lần lượt là số cây trồng được của lớp 7A1,7A2,7A3,7A4
(x,y,z,t ∈ N * )
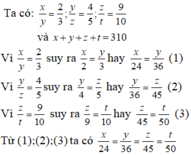
Với x + y + z + t = 172 , áp dụng tính chất dãy tỉ số bằng nhau ta có
x 24 = y 36 = z 45 = t 50 = x + y + z + t 24 + 36 + 45 + 50 = 310 155 = 2
Suy ra z 45 = 2 nên t = 45.2 = 90 (tm)
Số cây của lớp 7A4 trồng được là 90 cây
Đáp án cần chọn là B
S
5 tháng 9 2020
Trả lời :
Gọi số học sinh của lớp 7a1 và lớp 7a2 lần lượt là a, b.
Theo bài ta có :
b - a = 5
Mà a : b tỉ lệ với 8 : 9 \(\Leftrightarrow\frac{a}{8}=\frac{b}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được :
\(\frac{a}{8}=\frac{b}{9}=\frac{b-a}{9-8}=\frac{5}{1}=5\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{8}=5\\\frac{b}{9}=5\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a=40\\b=45\end{cases}}\)
KC
6 tháng 9 2020
- Gọi số học sinh của lớp 7A1 là \(x\) và số học sinh của lớp 7A2 là \(y\).
Theo đè bài ,ta có : \(y-x=5\)
Áp dụng tính chất dãy tỉ số bằng nhau . Ta có :
\(\frac{y}{9}-\frac{x}{8}=\frac{y-x}{9-8}=\frac{5}{1}=5\)
+) \(\frac{y}{9}=5\Rightarrow y=45\)
+) \(\frac{x}{8}=5\Rightarrow x=40\)
Vậy số học sinh của lớp 7A1 và 7A2 lần lượt là 40 và 45 hs .
22 tháng 10 2021
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{6}=\dfrac{c}{4}=\dfrac{a+b+c}{5+6+4}=\dfrac{180}{15}=12\)
Do đó: a=60; b=72; c=48
DN
5 tháng 3 2023
cho tam giác ABC vuông tại A có AB=AC gọi K là trung điểm của cạnh BC a,Chứng minh Tam giác AKB=Tam giác AKC và AK vuông góc BC b,Từ C kẻ đường vuông góc với BC cắt AB tại E.Chứng minh AK//CE và CE=CB c, So sánh AK và CE
Gọi số hs giỏi lớp 7A0;7A1;7A2 lần lượt là \(a,b,c\left(a,b,c\in N\text{*}\right)\left(hs\right)\)
Vì số học sinh giỏi của ba lớp 7A0, 7A1, 7A2 tỉ lệ với 3;5;7 nên \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\)
Mà số học sinh giỏi của lớp 7A0 nhiều hơn số học sinh giỏi của lớp 7A2 là 12 học sinh nên \(a-c=12\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a-c}{3-7}=\dfrac{12}{-4}=-8\) (vô lí)
Vậy đề sai