Cho đường tròn có tâm O và điểm M nằm ngoài đuờng tròn. MO cắt (O) tại E và F (ME<MF).Vec cát tuyến MAB và tiếp tuyến MC cuả (O) (C là tiếp điểm<A nằm giữa M và B,A và C nằm khác phía đối với MO)a) Gọi H là hình chiếu vuông góc của C lên MO. Trên nữa mặt phẳng MO có chứa điểm A, vẽ nữa đường tròn đường kính MF cắt tiếp tuyến tại E của (O) ở K. S là giao điểmcủa CO và KF. CM:...
Đọc tiếp
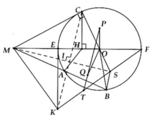
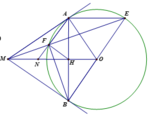
Cho đường tròn có tâm O và điểm M nằm ngoài đuờng tròn. MO cắt (O) tại E và F (ME<MF).Vec cát tuyến MAB và tiếp tuyến MC cuả (O) (C là tiếp điểm<A nằm giữa M và B,A và C nằm khác phía đối với MO)
a) Gọi H là hình chiếu vuông góc của C lên MO. Trên nữa mặt phẳng MO có chứa điểm A, vẽ nữa đường tròn đường kính MF cắt tiếp tuyến tại E của (O) ở K. S là giao điểmcủa CO và KF. CM: MS \(\perp\)KC
b) P và Q lần lượt là tâm của đường tròn ngoại tiếp tam giác EFS và ABS.T là trung điểm của KS. CM P,P,T thẳng hàng.
Mai mình nộp bài giúp với.
a) Theo tính chất góc tạo bởi tia tiếp tuyến và dây thì ^MCE = ^MFC (Cùng chắn cung CE)
Suy ra: \(\Delta\)MEC ~ \(\Delta\)MCF (g.g) => MC2 = ME.MF (1)
Ta thấy: ^MKF = 900 (Góc nội tiếp chắn nửa đường tròn) => \(\Delta\)KMF vuông ở K
Xét \(\Delta\)KMF vuông tại K có đường cao KE => MK2 = ME.MF (2) (Hệ thức lượng trong tg vuông)
Từ (1) và (2) => MC = MK. Khi đó: \(\Delta\)MCS và \(\Delta\)MKS có: ^MCS = ^MKS (=900), MC=MK, SM cạnh chung
=> \(\Delta\)MCS = \(\Delta\)MKS (Cạnh huyền . Cạnh góc vuông) => CS = KS. Do đó MS là trung trực của CK
Hay MS vuông góc với KC (đpcm).
b) Gọi giao điểm của MS và KC là I. Theo hệ thức lượng: MC2 = MI.MS = ME.MF = MA.MB
=> Các tứ giác BAIS và SIEF nội tiếp => 2 đường tròn (P) và (Q) có 2 điểm chung là I và S
=> PQ là trung trực của IS => PQ vuông góc với IS tại trung điểm của IS. Mà IS vuông góc CK
Nên PQ // CK. Từ đó: PQ nằm trên đường thẳng chứa đường trung bình của \(\Delta\)CKS (PQ //CK)
Vậy thì PQ đi qua trung điểm của KS. Hay PQ đi qua T => 3 điểm P,Q,T thẳng hàng (đpcm).