Có bao nhiêu tiếp tuyến với đồ thị (C): \(y=x^3-3x^2+2\) song song với đường thẳng y=9x-25
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 12 2018
Chọn B.
y' = x2 – 4x + 3
Tiếp tuyến của (C) tại M là 
D ss với đt y = 3x + 1 khi
Với 2 giá trị của m suy ra 2 tiếp tuyến.
CM
8 tháng 1 2018
Chọn D.
Ta có: y’ = -3x2 + 6x. Lấy điểm M(xo; yo) ∈ (C).
Tiếp tuyến tại Msong song với đường thẳng y = -9x suy ra y’(xo) = -9
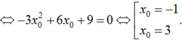
Với xo = -1 ⇒ yo = 2 ta có phương trình tiếp tuyến: y = -9x - 7
Với xo = 3 ⇒ yo = -2 ta có phương trình tiếp tuyến: y = -9x + 25
Vậy có 2 tiếp tuyến thỏa mãn.
CM
15 tháng 2 2019
- Tập xác định: D = R.
- Đạo hàm: y ' = 3 x 2 - 6 x .
- Đường thẳng d: y = 9x + 100 có hệ số góc k = 9.
- Vì tiếp tuyến song song với đường thẳng d nên k t t = 9 .
- Ta có:
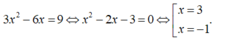
- Vậy có 2 tiếp tuyến thỏa mãn yêu cầu bài toán.
Chọn C
Tiếp tuyến \(y=kx+b\) qua 1 điểm \(A\left(x_0;y_0\right)\) bất kì thuộc (C) có hệ số góc
\(k=f'\left(x_0\right)=3x_0^2-6x_0\)
Để tiếp tuyến song song với \(y=9x-25\)
\(\Rightarrow\) \(\left\{{}\begin{matrix}k=9\\b\ne-25\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}3x_0^2-6x_0=9\\x_0^3-3x_0^2+2\ne25\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=-1\\x_0=3\end{matrix}\right.\)
\(\Rightarrow\) có 2 tiếp tuyến thỏa mãn
c ơi t làm ra 1 tiếp tuyến tm thôi