Rut gon P = \(\dfrac{3+\sqrt{5}}{2\sqrt{2}+\sqrt{3+\sqrt{5}}}+\dfrac{3-\sqrt{5}}{2\sqrt{2}-\sqrt{3-\sqrt{5}}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{-\left(\sqrt{x}+1\right)\left(2+\sqrt{x}\right)-2\sqrt{x}\left(2-\sqrt{x}\right)+5\sqrt{x}+2}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}:\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(\sqrt{x}+2\right)^2}\)
\(A=\dfrac{-3\sqrt{x}-x-2-4\sqrt{x}+2x+5\sqrt{x}+2}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(A=\dfrac{-x-2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(A=\dfrac{-\sqrt{x}\left(\sqrt{x}+2\right)^3}{\left(\sqrt{x}+2\right)\left(2-\sqrt{x}\right)\sqrt{x}\left(3-\sqrt{x}\right)}=\dfrac{-\left(\sqrt{x}+2\right)^2}{\left(2-\sqrt{x}\right)\left(3-\sqrt{x}\right)}\)

\(P=\dfrac{\left(\sqrt{a+1}+1\right)\left(\sqrt{a+1}+2\right)}{\left(\sqrt{a+1}-2\right)\left(\sqrt{a+1}+2\right)}+\dfrac{2\sqrt{a+1}\left(\sqrt{a+1}-2\right)}{\left(\sqrt{a+1}-2\right)\left(\sqrt{a+1}+2\right)}-\dfrac{2+5\sqrt{a+1}}{a-3}\)
\(P=\dfrac{a+3+3\sqrt{a+1}}{a-3}+\dfrac{2a+2-4\sqrt{a+1}}{a-3}-\dfrac{2+5\sqrt{a+1}}{a-3}\)
\(P=\dfrac{a+3+3\sqrt{a+1}+2a+2-4\sqrt{a+1}-2-5\sqrt{a+1}}{a-3}\)
\(P=\dfrac{3a+3-6\sqrt{a+1}}{a-3}\)
Có thể dừng ở đây hoặc nếu thích thì làm tiếp như sau (chưa chắc gọn hơn):
\(P=\dfrac{3\left(a+1\right)-6\sqrt{a+1}}{\left(\sqrt{a+1}-2\right)\left(\sqrt{a+1}+2\right)}=\dfrac{3\sqrt{a+1}\left(\sqrt{a+1}-2\right)}{\left(\sqrt{a+1}-2\right)\left(\sqrt{a+1}+2\right)}\)
\(P=\dfrac{3\sqrt{a+1}}{\sqrt{a+1}-2}\)

Cho \(5\sqrt{x}7\) mk viet nham
Sua lai thanh \(5\sqrt{x}-7\)
a: \(A=\left(\dfrac{2}{\sqrt{x}-2}+\dfrac{3}{2\sqrt{x}+1}-\dfrac{5\sqrt{x}-7}{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\right)\cdot\dfrac{5\sqrt{x}\left(\sqrt{x}-2\right)}{2\sqrt{x}+3}\)
\(=\dfrac{4\sqrt{x}+2+3\sqrt{x}-6-5\sqrt{x}+7}{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{5\sqrt{x}\left(\sqrt{x}-2\right)}{2\sqrt{x}+3}\)
\(=\dfrac{2\sqrt{x}+3}{\left(2\sqrt{x}+1\right)}\cdot\dfrac{5\sqrt{x}}{2\sqrt{x}+3}=\dfrac{5\sqrt{x}}{2\sqrt{x}+1}\)
b: Để A là số nguyên thì \(5\sqrt{x}⋮2\sqrt{x}+1\)
=>10 căn x+5-5 chia hết cho 2 căn x+1
=>\(2\sqrt{x}+1\in\left\{1;5\right\}\)
hay \(x\in\varnothing\)

a: \(A=\left(2\sqrt{5}-3\sqrt{5}+3\sqrt{5}\right)\cdot\sqrt{5}=2\sqrt{5}\cdot\sqrt{5}=10\)
\(B=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}-1+\sqrt{x}=2\sqrt{x}-1\)
b: A=2B
=>\(10=4\sqrt{x}-2\)
=>\(4\sqrt{x}=12\)
=>x=9(nhận)

\(\dfrac{2\sqrt{x}}{x-5\sqrt{x}+6}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{\sqrt{x}+3}{2-\sqrt{x}}\left(ĐK:x\ge0;x\ne4;x\ne9\right)\)
\(=\dfrac{2\sqrt{x}}{x-2\sqrt{x}-3\sqrt{x}+6}+\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)-3\left(\sqrt{x}-2\right)}+\dfrac{2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{x-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}+2x-3\sqrt{x}-2-x+9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-\sqrt{x}+7}{x-5\sqrt{x}+6}\)
#Urushi

\(\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{\sqrt{x}+3}{2-\sqrt{x}}\) (ĐK: \(x\ne9;x\ne4;x\ge0\))
\(=\dfrac{2\sqrt{x}-9}{x-2\sqrt{x}-3\sqrt{x}+6}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}-9}{\sqrt{x}\left(\sqrt{x}-2\right)-3\left(\sqrt{x}-2\right)}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-9+2x-4\sqrt{x}+\sqrt{x}-2-x+9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-2\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
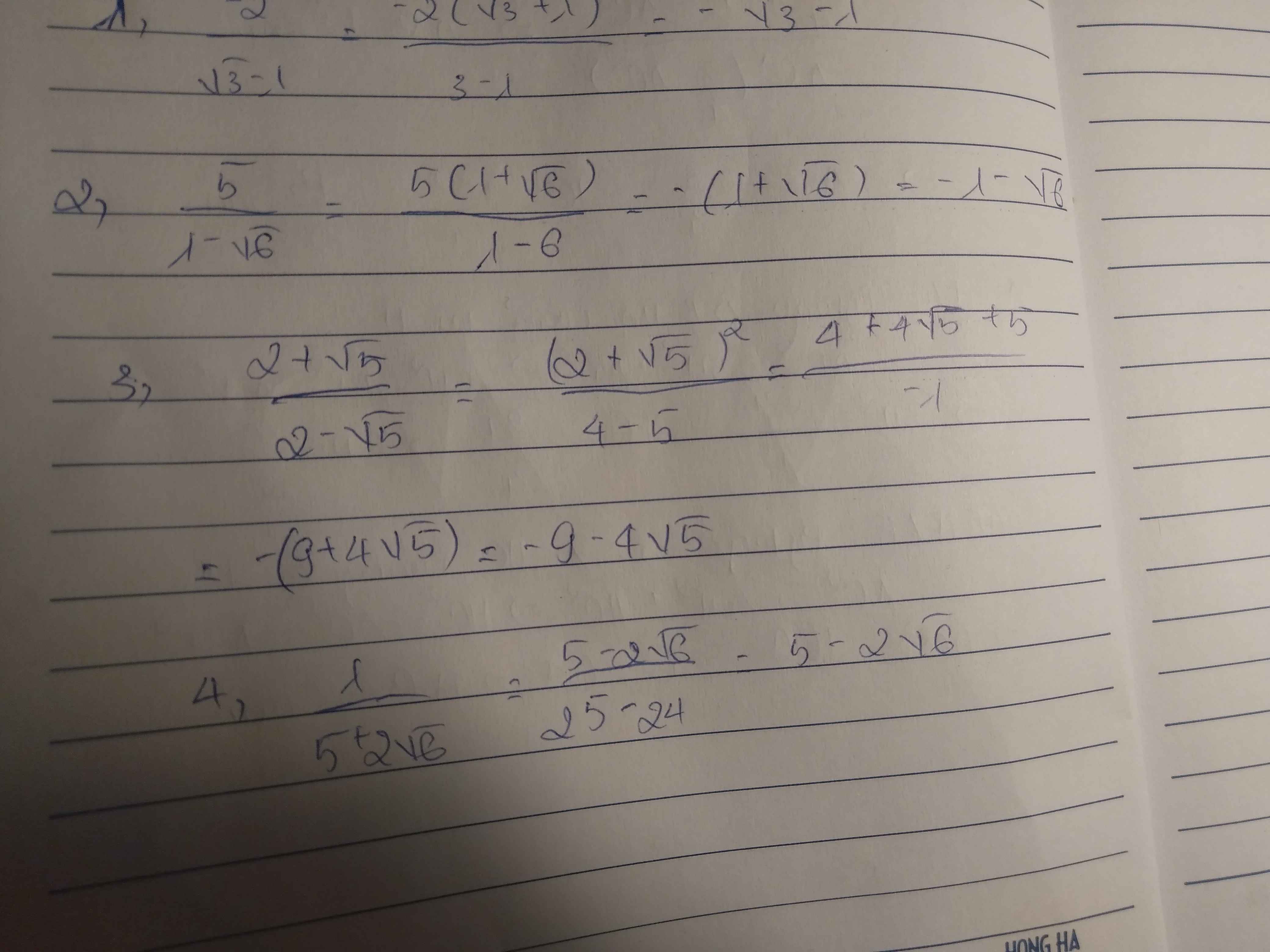
\(P=\dfrac{\sqrt{2}\left(3+\sqrt{5}\right)}{\sqrt{2}\left(2\sqrt{2}+\sqrt{3+\sqrt{5}}\right)}+\dfrac{\sqrt{2}\left(3-\sqrt{5}\right)}{\sqrt{2}\left(2\sqrt{2}-\sqrt{3-\sqrt{5}}\right)}\)
\(=\dfrac{3\sqrt{2}+\sqrt{10}}{4+\sqrt{6+2\sqrt{5}}}+\dfrac{3\sqrt{2}-\sqrt{10}}{4-\sqrt{6-2\sqrt{5}}}\)
\(=\dfrac{3\sqrt{2}+\sqrt{10}}{5+\sqrt{5}}+\dfrac{3\sqrt{2}-\sqrt{10}}{5-\sqrt{5}}\)
\(=\dfrac{\left(3\sqrt{2}+\sqrt{10}\right)\left(5-\sqrt{5}\right)+\left(3\sqrt{2}-\sqrt{10}\right)\left(5+\sqrt{5}\right)}{20}\)
\(=\dfrac{15\sqrt{2}-3\sqrt{10}+5\sqrt{10}-5\sqrt{2}+15\sqrt{2}+3\sqrt{10}-5\sqrt{10}-5\sqrt{2}}{20}\)
\(=\dfrac{30\sqrt{2}-10\sqrt{2}}{20}=\dfrac{20\sqrt{2}}{20}=\sqrt{2}\)
\(\)