cho hình thoi ABCD có \(A=60^o\).Diện tích là \(2\sqrt{3}cm^2\).Cạnh AB=?.(tự vẽ hình ra nháp.chỉ cần nêu lời giải thuj)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cạnh hình thoi ABCD là : 60 : 4 = 15 (cm)
Hiệu độ dài MB và AM là 5 cm
Độ dài cạnh MB là: (15 + 5 ) : 2 = 10 (cm)
Độ dài cạnh AM là: 15 - 10 = 5 (cm)
a) Hình bình hành MBCN có: MB = NC = 10 cm; MN = BC = 15 cm
Chu vi hình MBCN là: 10 + 15 + 10 + 15 = 50 (cm)
b) Chiều cao hình thoi ABCD là: 216 : 15 = 14,4 (cm)
Chiều cao hình bình hành AMND bằng chiều cao hình thoi ABCD ; có đáy là AM
Diện tích hình bình hành AMND là: 14,4 x 5 = 72 (cm2)
A)Hiệu độ dài MB và AM là 5 cm
Độ dài cạnh AM là: 15 - 10 = 5 cm
Chu vi hình MBCN là: MB + BC + CN + NM = 10 + 15 + 10 + 15 = 50 cm
B)Chiều cao hình bình hành AMND bằng chiều cao hình thoi ABCD ; có đáy là AM.

Đặt AB = x
Gọi AC giao BD tại O
Tam ABD có AB = AD và A = 60 độ
=> tam giác ABD đều => AB = BD = x
BAC = 1/2 BAD = 1/2 . 60 = 30 độ ( AC là pg )
Tam giác ABO vuông tại O , theo HT giữa cạnh và góc
=> OA = AB . sin BAO = x.cos30 = \(\frac{\sqrt{3}}{2}x\)
=> AC = 2 OA = \(2\cdot\frac{\sqrt{3}}{2}x=\sqrt{3}x\)
\(S_{ABCD}=\frac{1}{2}AC\cdot BD=\frac{1}{2}\cdot x\cdot\sqrt{3}x=2\sqrt{3}\Leftrightarrow x^2=4\Leftrightarrow x=2\)

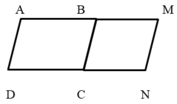
Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có :
BC = BM = MN = 3 cm
Chiều cao tương ứng cạnh DC của hình bình hành ABCD là :
8 : 4 = 2 (cm)
Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là :
3 x 2 = 6 (cm2)
Đáp số : 6 cm2
Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có :
BC = BM = MN = 3 cm
Chiều cao tương ứng cạnh DC của hình bình hành ABCD là :
8 : 4 = 2 (cm)
Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là :
3 x 2 = 6 (cm2) Đáp số:6 cm2

a: Xét ΔBAC có BA=BC và góc ABC=60 độ
nên ΔABC đều
=>\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(S_{ABCD}=\dfrac{a^2\sqrt{3}}{2}\)

Vì hình ABCD là hình bình hành nên cạnh AD = BC = 3cm. Vì hình BMNC là hình thoi nên có các cạnh bằng nhau, do đó ta có: BC = BM = MN = 3 cm Chiều cao tương ứng cạnh DC của hình bình hành ABCD là: 8 : 4 = 2 (cm) Chiều cao tương ứng cạnh DC cũng là chiều cao tương ứng cạnh NC do đó diện tích hình thoi BMNC là : 3 x 2 = 6 (cm2 ) Đáp số: 6 cm2

kẻhình thoi ABCD ta có
A=60o nên tam giác ABD đều nên AB=BD
kẻ AC cắt BD tại E
ta có SABCD=\(2\sqrt{3}\)=>\(\frac{1}{2}.BD.AC=2\sqrt{3}\Rightarrow\frac{1}{2}.AB.2AE=2\sqrt{3}\Rightarrow AB.AE=2\sqrt{3}\)
vì tam giác vuông ABE có B=60o
nên AE=\(\frac{\sqrt{3}}{2}.AB\) thế vào pt ta có
AB.AB.\(\frac{\sqrt{3}}{2}\)=\(2\sqrt{3}\)
\(AB^2=2\sqrt{3}:\frac{\sqrt{3}}{2}\Rightarrow AB^2=4\)
nên AB =2 vì AB dương