trên hai nửa mặt phẳng đối nhau, bờ t't ta vẽ hai tia Ox và Oy(O € tt') chứng tỏ rằng hoặc tia Ot hoặc tia Ot' nằm giữa hai tia Ox và Oy.
nhớ kẻ hình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

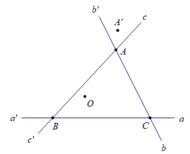
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.

a: Xét ΔKAC và ΔKPB có
KA=KP
\(\widehat{AKC}=\widehat{PKB}\)
KC=KB
Do đó:ΔKAC=ΔKPB
=>\(\widehat{KAC}=\widehat{KPB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//PB
b: \(\widehat{NAC}=\widehat{NAB}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\widehat{BAM}=\widehat{BAC}+\widehat{MAC}=90^0+\widehat{BAC}\)
Do đó: \(\widehat{BAM}=\widehat{NAC}\)
Xét ΔBAM và ΔNAC có
BA=NA
\(\widehat{BAM}=\widehat{NAC}\)
AM=AC
Do đó: ΔBAM=ΔNAC
=>BM=CN
c:
ΔKBP=ΔKCA
=>BP=AC
mà AC=AM
nên BP=AM
AC//BP
=>\(\widehat{ABP}+\widehat{BAC}=180^0\)(1)
\(\widehat{BAC}+\widehat{NAM}+\widehat{NAB}+\widehat{MAC}=360^0\)
=>\(\widehat{BAC}+\widehat{NAM}+90^0+90^0=360^0\)
=>\(\widehat{NAM}+\widehat{BAC}=180^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{ABP}=\widehat{NAM}\)
Xét ΔABP và ΔNAM có
AB=NA
\(\widehat{ABP}=\widehat{NAM}\)
BP=AM
Do đó: ΔABP=ΔNAM
em ơi viết lại hộ cái đề bài nha
Khách là em