Vẽ đường tròn tâm O bán kính 3 cm, vẽ dây AB Đi qua O
a. Tính độ dài dây AB
b. Lấy điểm I thuộc OA Sao cho OI=2cm, qua I kẻ dây AM vuông góc với AB. Tính độ dài dây MN
Giúp mks Vs ạ mai mks nộp r
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 8 2023
a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc AB
I là trung điểm của AB
=>IA=IB=16/2=8cm
ΔOIA vuông tại I
=>OA^2=OI^2+IA^2
=>OI^2=10^2-8^2=36
=>OI=6(cm)
b: OM=OI+IM
=>6+IM=10
=>IM=4cm
ΔMIA vuông tại I
=>MI^2+IA^2=MA^2
=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)
2 tháng 1 2022
b: Xét ΔMCO có
CA là đường trung tuyến
CA=OM/2
Do đó: ΔMCO vuông tại C
20 tháng 1 2023
ΔOAB cân tại O
mà OI là đường cao
nên I là trung điểm của AB
\(AI=\sqrt{10^2-6^2}=8\left(cm\right)\)
AB=2*8=16cm
CM
13 tháng 5 2019
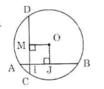
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
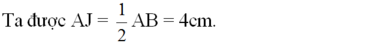
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có: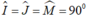 
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)
a: AB=2*OA=6cm
b: \(MI=\sqrt{3^2-2^2}=\sqrt{5}\left(cm\right)\)
=>\(MN=2\sqrt{5}\left(cm\right)\)