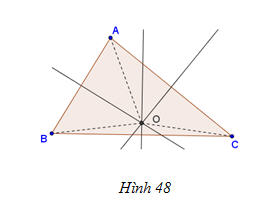
Cho tam giác ABC bất kì. Vẽ các đường thẳng trung trực của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 8 2017
a,vẽ tam giác ABC . Về các đường trung trực của các đoạn thẳng AB,BC,CA
b, vẽ đường tròn tâm O bán kính R=3 cm. lấy ba điểm A,B,C phân biệt bất kì trên đường tròn. về các dây AB,BC,CÁ. V e các đường trung trực của các đoạn thẳng AB,BC,CA
câu này mik chịu
8 tháng 3 2018
Gọi I là giao điểm của đường trung trực của BC với BC . Nối KC
Ta có tam giác EIC = tam giác EIB ( c.g.c )
=> CE = BE ( hai cạnh tương ứng )
chu vi tam giác AEB = AE + AB + BE = AE + AB + CE ( do BE = CE )
=> chu vi tam giác ABE = AB + AC ( do AE + CE = AC )
tam giác KIB = tam giác KIC ( c.g.c )
=> KB = KC ( hai cạnh tương ứng )
chu vi tam giác AKB = AK + BK + AB = AK + KC + AB ( do BK = CK )
xét tam giác ACK theo bất đẳng thức tam giác ta có
AK + CK > AC
=> AK + CK + AB > AC + AB
=> chu vi tam giác ABK > chu vi tam giác ABE
23 tháng 7 2023
a: ΔABC cân tại A
mà AE là phân giác
nên AE là trung trực của BC
b: O nằm trên trung trực của AB
=>OA=OB
O nằm trên trung trực của BC
=>OB=OC
=>OA=OC
=>O nằm trên trung trực của AC
c: OA=OB=OC
=>O cách đều 3 đỉnh của ΔABC
16 tháng 6 2017
A B C D E F H I K
DE//BC, AH vuông góc BC => AH vuông góc DE (Qhệ //, vuông góc) (1)
BC//AD, AC//BD => BC=AD, AC=BD (T/c đoạn chắn), tương tự BC=AE => BC=AD=AE (2)
Từ (1) và (2) => AH là trung trực của DE.
Tương tự với các cạnh của tam giác DEF và đường cao của tam giác ABC, ta có:
BI vuông góc DF, AC=BD=BF => BI là trung trực của DF
CK vuông góc EF, AB=CE=CF => CK là trung trực của EF.
Kết luận:...