Cho tam giác ABC vuông tại A trên nửa mặt phẳng bờ BC có chứa A vẽ tia Bx sao cho\(\widehat{ABx}\)= \(\widehat{ABC}\). Qua A vẽ đường thẳng d vuông góc với Bx tại D. Qua C vẽ đường thẳng vuông góc với d tại E.
CMR: AD=AE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
23 tháng 6 2020
Hình bạn tự vẽ nha
Kẻ AH\(\perp\)BC
Xét hai tam vuông ABD và tam giác vuông ABH có
góc ADB = góc AHB = 90độ
cạnh AB chung
góc ABD = góc ABH [ gt ]
Do đó ; tam giác ABD = tam giác ABH [ cạnh huyền - góc nhọn ]
\(\Rightarrow\)AD = AH [1] và góc DAB = góc HAB
mà góc HAB + góc CAH = 90độ
\(\Rightarrow\)góc DAB + góc CAH = 90độ
Mặt khác ; góc DAB + góc CAH + góc BAH + góc CAE = 180độ
\(\Rightarrow\)góc BAH + góc CAE = 180độ - 90độ = 90độ
\(\Leftrightarrow\)góc CAE = góc CAH [ cùng phụ với góc BAH ]
Xét hai tam giác vuông ACE và tam giác vuông ACH có
góc AEC = góc AHC = 90độ
cạnh AC chung
góc CAE = góc CAH [ theo chứng minh trên ]
Do đó ; tam giác ACE = tam giác ACH [ cạnh huyền - góc nhọn ]
\(\Rightarrow\)AE = AH [ 2 ]
Từ [ 1 ] và [ 2 ] suy ra ; AE = AD = AH
Vậy AE = AD
Học tốt
Nhớ ti ck cho mình nha
26 tháng 2 2020
Câu hỏi của son tung - Toán lớp 7 - Học toán với OnlineMath
5 tháng 1 2018
trên tia AC lấy điểm F sao cho À = AD
Nối D với C ; D với F
\(\Rightarrow\Delta ADF\)vuông cân tại A
\(\Rightarrow\widehat{ADF}=\widehat{AFD}=45^o\)
Mà \(\widehat{AFD}+\widehat{DFC}=180^o\)( 2 góc kề bù )
hay \(\widehat{DFC}=180^o-45^o=135^o\)
Xét \(\Delta ADC\)vuông tại A có :
\(\widehat{ADC}+\widehat{ACD}=90^o\)( 1 )
vì \(\widehat{ADC}+\widehat{CDE}+\widehat{EDB}=180^o\)
hay \(\widehat{ADC}+90^o+\widehat{EDB}=180^o\)
\(\Rightarrow\widehat{ADC}+\widehat{EDB}=90^o\)( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\widehat{ACD}=\widehat{EDB}\)
vì \(\Delta ABC\)vuông cân \(\Rightarrow AB=AC\)mà AB = AF
\(\Rightarrow BD=FC\)
Xét \(\Delta BDE\)và \(\Delta CFO\)có :
\(\widehat{ACD}=\widehat{EDB}\)( cmt )
BD = FC ( cmt )
\(\widehat{DFC}=\widehat{DBE}\)( = 135 độ )
Suy ra : \(\Delta BDE\)= \(\Delta CFO\)( g.c.g )
\(\Rightarrow\)DC = DE ( 2 cạnh tương ứng )
mà \(\widehat{CDE}\)= \(90^o\)
Suy ra : \(\Delta DEC\)là tam giác vuông cân
26 tháng 2 2020
Câu hỏi của son tung - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo!
LM
17 tháng 2 2016
Lấy F thuộc AC sao cho AD = AF. Khi đó tam giác ADF vuông cân ở A ==> DFAˆ=450→DFCˆ=1350
Ta có:
BDEˆ=1800−EDCˆ−ADCˆ=1800−900−ADCˆ=900−ADCˆ
ACDˆ=900−ADCˆ (vì tam giác ADC vuông ở A)
Suy ra ACDˆ=BDEˆ
Mặt khác:
BD = AB - AD
CF = AC - AF
AB = AC, AD = AF
Nên BD = CF.
Xét tam giác BDE và tam giác FCD:
BD = FC
BDEˆ=FCDˆ
EBDˆ=DFCˆ(=1350)
Suy ra ΔBDE = ΔFCD (g.c.g) ==> DE = DC
Mà tam giác EDC vuông ở D.
Suy ra tam giác EDC vuông cân ở D.
NX
9 tháng 8 2023
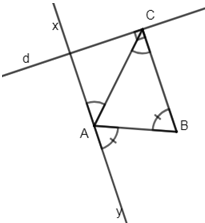
a) Ta có: mà hai góc đó là hai góc so le trong nên
suy ra (1)
mà hai góc đó là hai góc so le trong nên suy ra (2)
Từ (1) và (2) suy ra Ax và Ay cùng // BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
Ax và Ay là hai tia đối nhau.
b) Vì Ax và Ay là hai tia đối nhau (cmt) mà và
nên suy ra
Mà nên suy ra
A=x+5=11 chúc bạn học giỏi