Cho tam giác ABC vuông tại A có AB=AC. Trên cùng nửa mặt phẳng có bờ là BC chứa A. kẻ các tia Bx, Cy vuông góc với BC. Gọi M là điểm thuộc canh BC ( M \(\ne\)B,C ). Đường thẳng vuông góc với AM tại A cắt BX, Cy lần lượt tại D, E. Lấy I nằm giữa A và D. Kẻ HE vuông góc với MI. Chứng minh rằng: HA là phân giác của \(\widehat{EHI}\). MẤY BẠN GIÚP MÌNH VỚI Ạ. MÌNH CẦN GẤP. AI ĐÚNG MÌNH SẼ TICK!!!! Thank you!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 1 2022
1c (2 câu kia em tự giải)
Kẻ đường cao AH \(\Rightarrow\) AH cố định
Do \(\widehat{MAF}\) và \(\widehat{MCF}\) cùng nhìn MF dưới 1 góc vuông nên tứ giác MAFC nội tiếp
\(\Rightarrow\widehat{AFM}=\widehat{ACM}\) (cùng chắn AM)
\(\Rightarrow\Delta_VFME\sim\Delta_VCAB\left(g.g\right)\) với tỉ số đồng dạng \(k=\dfrac{AM}{AH}\)
\(\Rightarrow S_{MEF}=k^2.S_{ABC}\Rightarrow S_{MEF-min}\) khi \(k_{min}\)
Mà trong tam giác vuông AHM ta có \(AH\le AM\Rightarrow k\ge1\Rightarrow k_{min}=1\) khi M trùng H
Hay diện tích MEF min khi M là chân đường cao từ A xuống BC
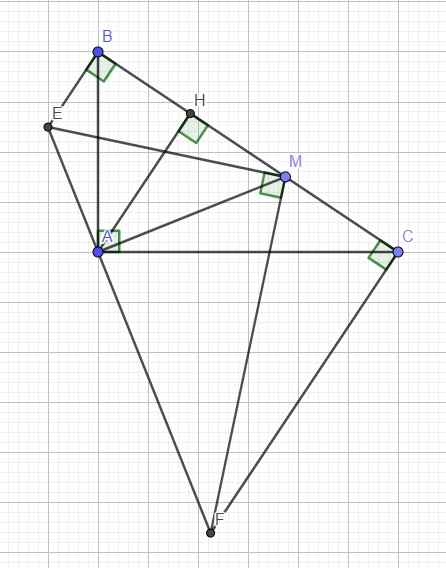
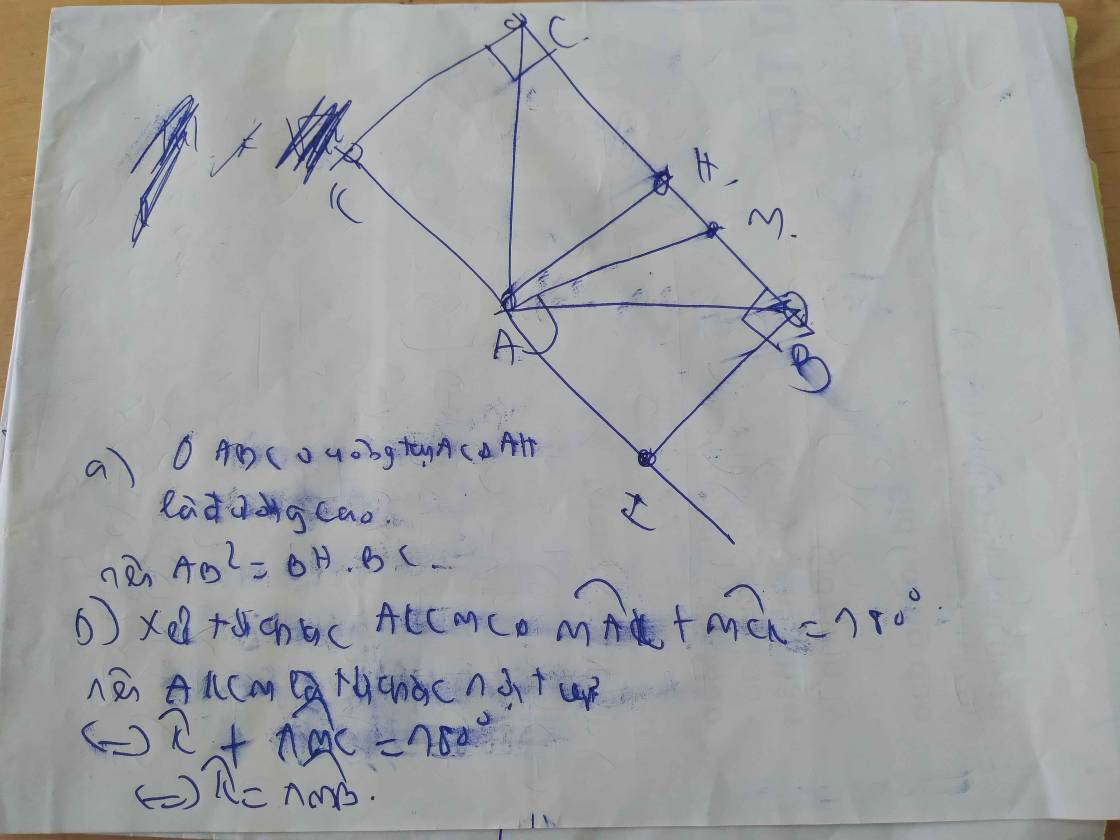


Đường thẳng vuông góc với AM tại A cắt BX, Cy lần lượt tại D, E