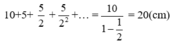Có 70 hình vuông cạnh 1 cm. Hỏi có thể xếp được một hình vuông có cạnh lớn nhất bằng bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Để tìm số lượng hình vuông có thể cắt được và độ dài cạnh của mỗi hình vuông, chúng ta cần tìm ước chung lớn nhất (UCLN) của chiều dài và chiều rộng của tờ bìa.
Chiều dài của tờ bìa là 120cm và chiều rộng là 90cm. Ta có thể tìm UCLN của 120 và 90 bằng cách sử dụng thuật toán Euclid:
120 = 90 × 1 + 30
90 = 30 × 3 + 0
Do đó, UCLN của 120 và 90 là 30.
Vì vậy, ta có thể cắt tờ bìa thành các hình vuông có cạnh dài 30cm. Để tính số lượng hình vuông, ta chia chiều dài của tờ bìa cho độ dài cạnh hình vuông:
120cm / 30cm = 4
Vậy, ta có thể cắt được 4 hình vuông có cạnh dài 30cm từ tờ bìa.

Gọi x (cm) là độ dài cạnh hình vuông lớn nhất có thể chia (x ∈ ℕ*)
⇒ x = ƯCLN(140; 60)
Ta có:
140 = 2².5.7
60 = 2².3.5
⇒ x = ƯCLN(140; 60) = 2².5 = 20
Vậy cạnh hình vuông lớn nhất có thể chia là 20 cm

Chọn B
Tổng các cạnh nằm trên tia Ax của các hình vuông đó là
10 + 5 + 5 2 + 5 2 2 + . . . = 20 ( c m )

Chọn B
Tổng các cạnh nằm trên tia Ax của các hình vuông đó là