1) Cho tam giác ABC nhọn có AB<AC, các đường cao BD và CE cắt nhau tại H, I là trung điểm của BC. Gọi K là điểm điểm đối xứng với H qua I, M là điểm đối xứng với H qua đường thẳng BC.
a, Các tứ giác BHCK, BCKM là hình gì ?
b, Gọi O là trung điểm của AK. Chứng minh O là giao điểm ba đường trung trực của tam giác ABC.
c, Chứng minh rằng AK vuông góc với DE.
2) Cho hai số a,b thỏa mãn đẳng thức a3 + b3 + 3(...
Đọc tiếp
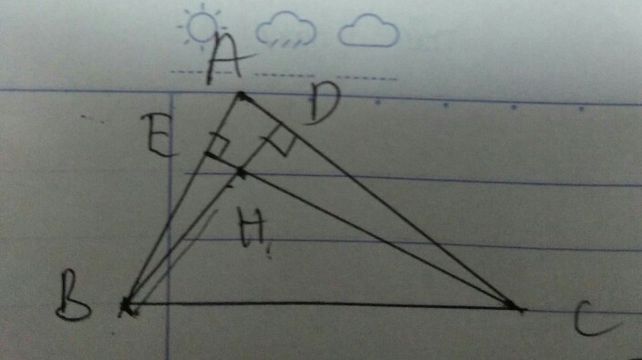
1) Cho tam giác ABC nhọn có AB<AC, các đường cao BD và CE cắt nhau tại H, I là trung điểm của BC. Gọi K là điểm điểm đối xứng với H qua I, M là điểm đối xứng với H qua đường thẳng BC.
a, Các tứ giác BHCK, BCKM là hình gì ?
b, Gọi O là trung điểm của AK. Chứng minh O là giao điểm ba đường trung trực của tam giác ABC.
c, Chứng minh rằng AK vuông góc với DE.
2) Cho hai số a,b thỏa mãn đẳng thức a3 + b3 + 3( a2 + b2 ) + 4( a + b ) + 4 = 0.Tính giá trị của biểu thức M = 2018( a + b )2
Câu 1:
a: Gọi N là giao của HM và BC
=>HM vuông góc với BC tại N và N là trung điểm của HM
Xét tứ giác BHCK co
I là trung điểm chung của BC và HK
nên BHCK là hình bình hành
Xét ΔHMK có HN/HM=HI/HK
nên IN//MK
=>BC//MK
Xét tứ giác BCKM có
KM//BC
BK=CH
Do đó: BCKM là hình thang cân
b: BHCKlà hình bình hành
nên BH//CK; BK//CH
=>AB vuông góc với BK; AC vuông góc với CK
ΔBAK vuông tại B
mà BO là đường trung tuyến
nên BO=AO(1)
ΔCAK vuông tại C
mà CO là trung tuyến
nên CO=AO(2)
Từ (1), (2) suy ra BO=AO=CO