Tìm hệ số lớn nhất trong khai triển sau (x5 + 1/2x2)7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
1 tháng 3 2018
Đáp án C
Phương pháp:
Phân tích đa thức 1 + x + x 2 + x 3 thành nhân tử.
Sử dụng khai triển nhị thức Newton:
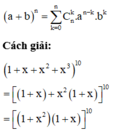
Áp dụng khai triển nhị thức Newton ta có:
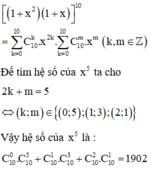


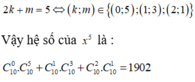


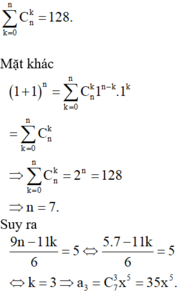
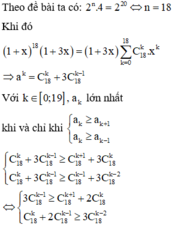
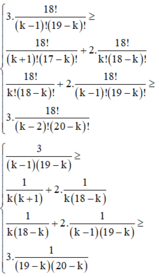


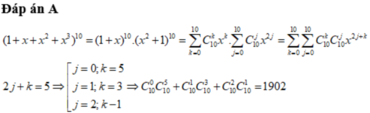
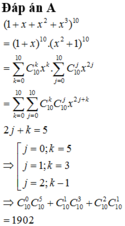
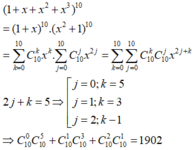
Có \(\left(x^5+\dfrac{1}{2}x^2\right)^7=\sum\limits^7_{k=0}.C^k_7.x^{35-5k}.2^{-k}.x^{2k}\\ =\sum\limits^7_{k=0}.C^k_7.2^{-k}.x^{35-3k}\)
Tìm hệ số lớn nhất, tức là ta phải tìm giá trị lớn nhất của ak = \(C^k_7.2^{-k}\) ( k ∈ { 0;1;2;3;4;5;6;7}
ak+1 = \(C^{k+1}_7.2^{-k+1}\)(k ∈ {0;1;2;3;4;5;6}
+) Xét ak < ak+1 (k ∈ {0;1;2;3;4;5;6}
\(< =>C^k_7.2^{-k}< C^{k+1}_7.2^{-k+1}\\ < =>\dfrac{7!}{k!\left(7-k\right)!}< \dfrac{7!.2}{\left(k+1\right)!\left(6-k\right)!}\\ < =>\dfrac{1}{\left(7-k\right)}< \dfrac{2}{\left(k+1\right)}\\ < =>\left(k+1\right)< 14-2k\\ < =>k< 4,33\\ =>\left\{{}\begin{matrix}k< 4,33\\k\in0;1;2;3;4;5;6\\k\in N\end{matrix}\right.=>k\in0;1;2;3;4\)
Do đó: a0 < a1 < a2 < a3 < a4 < a5 (1)
+) Xét ak > ak+1
\(< =>\left(k+1\right)>14-2k\\ < =>k>4,33\\ =>\left\{{}\begin{matrix}k>4,33\\k\in0;1;2;3;4;5;6\\k\in N\end{matrix}\right.=>k\in5;6\)
Do đó a5 > a6 (2)
Từ (1) và (2) => giá trị lớn nhất của a0 ; a1 ; a2 ;...; a7 là a5.
Vậy hệ số lớn nhất trong khai triển là a5