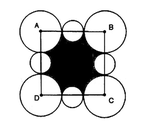
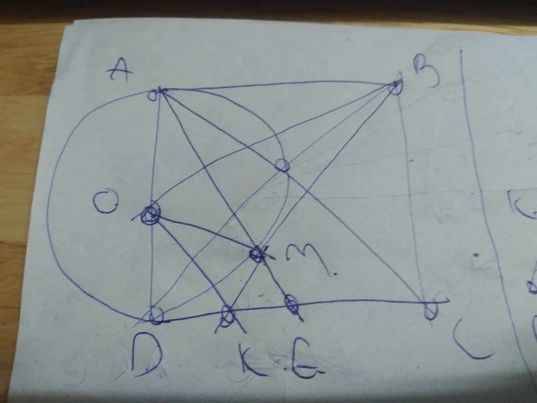
Cho hình vuông ABCD có cạnh bằng 1 , Vẽ\(\frac{1}{4}\)đường tròn tâm (A;1) nằm trong hình vuông , trên đó lấy điểm K . Vẽ tiếp tuyến tại K với đường tròn cắt cạnh BC tại E, cắt CD tại F .
a) tình góc EAF
b) AE cắt DK tại P , AF cắt DK tại Q. Cm PQ//BD và tính PQ?