Nhà ga số 1 và nhà ga số 2 của một sân bay có thể tiếp nhận tương ứng khoảng 6 526 300 và 3 514 500 lượt hành khách mỗi năm. Nhờ đưa vào sử dụng nhà ga số 3 mà mỗi năm sân bay này có thể tiếp nhận được khoảng 22 851 200 lượt hành khách. Hãy tính số lượt hành khách mà nhà ga số 3 có thể tiếp nhận mỗi năm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng số lượt hành khách mà nhà ga số 1 và số 2 có thể tiếp nhận mỗi năm là:
6 526 300 + 3 514 500 = 10 040 800 (lượt)
Số lượt hành khách mà nhà ga số 3 có thể tiếp nhận mỗi năm là:
22 851 200 – 10 040 800 = 12 810 400 (lượt)
Đáp số: 12 810 400 lượt hành khách
Lời giải:
Tổng số lượt hành khách mà nhà ga số 1 và số 2 có thể tiếp nhận mỗi năm là:
6 526 300 + 3 514 500 = 10 040 800 (lượt)
Do tổng số khách cả ba nhà ga mà sân bay có thể tiếp nhận mỗi năm khoảng 22 851 200 lượt khách hàng nên
Số lượt hành khách mà nhà ga số 3 có thể tiếp nhận mỗi năm là:
22 851 200 - 10 040 800 = 12 810 400 (lượt)
Đáp số: 12 810 400 lượt hành khách.

Số lượt khách nhà ga số 3 tiếp nhận được:
22851200-6526300-3514500=12810400 người

Tổng số lượt hành khách mà nhà ga số 1 và số 2 có thể tiếp nhận mỗi năm là:
6 526 300 + 3 514 500 = 10 040 800 (lượt)
Số lượt hành khách mà nhà ga số 3 có thể tiếp nhận mỗi năm là:
22 851 200 - 10 040 800 = 12 810 400 (lượt)
Đáp số: 12 810 400 lượt hành khách.

Mỗi hành khách có 4 cách chọn 1 toa để lên tàu nên số cách 4 hành khách chọn toa để lên tàu là 4 4 = 256 cách. Suy ra n Ω = 256
Gọi A là biến cố: “một toa có 3 hành khách; một toa có 1 hành khách và hai toa không có hành khách”.
Chon 3 hành khách từ 4 hành khách và xếp 3 hành khách vừa chọn lên 1 trong 4 toa tàu có C 5 3 . 4 = 16 cách
Xếp hành khách còn lại lên 1 trong 3 toa tàu còn lại có 3 cách
Suy ra n(A) = 16 . 3 = 48
Vậy xác suất của biến cố cần tìm là P A = 48 256 = 3 16
Đáp án B

Đáp án B
Mỗi hành khách có 4 cách chọn 1 toa để lên tàu nên số cách 4 hành khách chọn toa để lên tàu là ![]() cách. Suy ra
cách. Suy ra ![]()
Gọi A là biến cố: “một toa có 3 hành khách; một toa có 1 hành khách và hai toa không có hành khách”.
Chon 3 hành khách từ 4 hành khách và xếp 3 hành khách vừa chọn lên 1 trong 4 toa tàu có ![]() cách
cách
Xếp hành khách còn lại lên 1 trong 3 toa tàu còn lại có 3 cách
Suy ra ![]()
Vậy xác suất của biến cố cần tìm là
![]()

Mỗi hành khách có 3 lựa chọn \(\Rightarrow n\left(\Omega\right)=3^{12}\)
Chọn 4 người lên toa 1: \(C_{12}^4\) cách
Còn lại 8 người lên 2 toa còn lại, có \(2^8\) cách
Xác suất: \(\dfrac{C_{12}^4.2^8}{3^{12}}=...\)

Mỗi một cách lên toa thỏa yêu cầu bài toán chính là một hoán vị của 7 phần từ nên ta có: ![]()
Do đó: 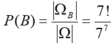
Chọn D.
giúp:(
Tổng số hành khánh mà nhà ga số 1 và 2 tiếp nhận mỗi năm là: \(6526300+3514500=10040800\)(hành khách)
Số lượt hành khách mà nhà ga số 3 tiếp nhận: \(22851200-10040800=12810400\)(lượt)