Cho đa giác đều (H) có 16 đỉnh. Chọn ngẫu nhiên 3 đỉnh trong 16 đỉnh của (H). Xác suất để 3 đỉnh được chọn tạo thành một tam giác vuông là ?
Giúp tớ với. Cảm ơn ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 10 2017
Số phần tử không gian mẫu:
.
(chọn 3 đỉnh bất kì từ 12 đỉnh của đa giác ta được một tam giác)
Gọi A: 3 đỉnh được chọn tạo thành tam giác đều ”.
(Chia 12 đỉnh thành 3 phần. Mỗi phần gồm 4 đỉnh liên tiếp nhau. Mỗi đỉnh của tam giác đều ứng với một phần ở trên.Chỉ cần chọn 1 đỉnh thì 2 đỉnh còn lại xác định là duy nhất).
Ta có: 
.
Khi đó: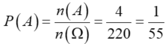 
.
Chọn A.
CM
7 tháng 11 2018
Số phần tử của không gian mẫu là số cách chọn 4 đỉnh trong 32 đỉnh để tạo thành tứ giác, Ω = C 32 4
Gọi A là biến cố "chọn được hình chữ nhật".
Để chọn được hình chữ nhật cần chọn 2 trong 16 đường chéo đi qua tâm của đa giác, do đó số phần tử của A là C 16 2
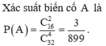
Chọn D
CM
10 tháng 12 2018
Đáp án D
Số phần tử của không gian mẫu là số cách chọn 4 đỉnh trong 32 đỉnh để tạo thành tứ giác, Ω = C 32 4
Gọi A là biến cố "chọn được hình chữ nhật".
Để chọn được hình chữ nhật cần chọn 2 trong 16 đường chéo đi qua tâm của đa giác, do đó số phần tử của A là C 16 2 .
TS
23 tháng 4 2023
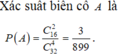
Phát biểu a) là phát biểu sai. Vì một tam giác đều khi có ba cạnh bằng nhau không nhất thiết phải bằng 2cm, có thể bằng 3cm, 4cm, …
Phát biểu b) là đúng. Vì tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau.
Phát biểu c) là sai. Vì tam giác IKH chỉ có hai cạnh và hai góc bằng nhau nên chưa đủ điều kiện để tam giác IKH là tam giác đều.
H9
HT.Phong (9A5)
CTVHS
28 tháng 3 2023
Do trong đội chỉ có một bạn nam và năm bạn nữ tổng tất cả bạn trong đội là 6
Vậy xác suất của biến cố bạn Nam được chon là: \(\dfrac{1}{6}\)
Không gian mẫu: \(n\left(\Omega\right)=C_{16}^3=560\)
Gọi O là tâm (H), chọn 2 đỉnh của (H) sao cho đoạn thẳng nối chúng đi qua O có 8 cách chọn (1)
Với mỗi đỉnh còn lại của (H), chúng sẽ cùng với hai điểm ở (1) tạo thành một tam giác vuông \(\Rightarrow\) còn lại 14 đỉnh
\(\Rightarrow\) có \(14.8=112\) tam giác vuông
Xác suất: \(P=\dfrac{112}{560}=\dfrac{1}{5}\)