1) Hình vuông ABCD. Phía trong hình dựng góc Bax = góc CDy = 75 độ. Ax cắt Dy tại N.
CMR : a, tam giác ABN, tam giác DCN cân và bằng nhau.
b, tam giác NDC đều.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 8 2017
BN CÓ THỂ GIẢI THEO 1 TRONG 3 CÁCH SAU
- CÁCH 1:
- vẽ tam giác đều ADK(K và B cùng phía với AD)
- =>ˆDAKDAK^=60∘60∘=>ˆKABKAB^=90∘90∘-60∘=30∘60∘=30∘.
- ΔABKΔABK cân tại A=>ˆABK=75∘ABK^=75∘=>KBC=90∘−75∘=15∘90∘−75∘=15∘
- tương tự
- ΔDKCΔDKCcân tại D=>ˆDKC=180∘−30∘2=75∘DKC^=180∘−30∘2=75∘=>ˆKCB=15∘KCB^=15∘
- có ΔAEB=ΔBKCΔAEB=ΔBKC(g.c.g)=>AE=BK=KCΔADE=ΔKDCΔADE=ΔKDC(c.g.c)
- =>DE=DC(1), ˆADE=ˆKDC=30∘ADE^=KDC^=30∘=>ˆEDC=60∘EDC^=60∘ (2)
(1),(2)→ΔEDC đều
- CÁCH 2
- Dựng tam giác đều DME (M trong tam giác ADE)
- MDA=15∘⇒ΔADM=ΔCDE(c.g.c)⇒AM=CE=DE=DM⇒ˆMAD=15∘⇒ˆAMD=150∘⇒ˆAME=150∘⇒ΔAMD=ΔAME(c.g.c)⇒AE=AD=AB⇒MDA^=15∘⇒ΔADM=ΔCDE(c.g.c)⇒AM=CE=DE=DM⇒MAD^=15∘⇒AMD^=150∘⇒AME^=150∘⇒ΔAMD=ΔAME(c.g.c)⇒AE=AD=AB
- Tính được ˆBAE=60∘→BAE^=60∘→ tam giác ABE là tam giác đều
- CÁCH 3
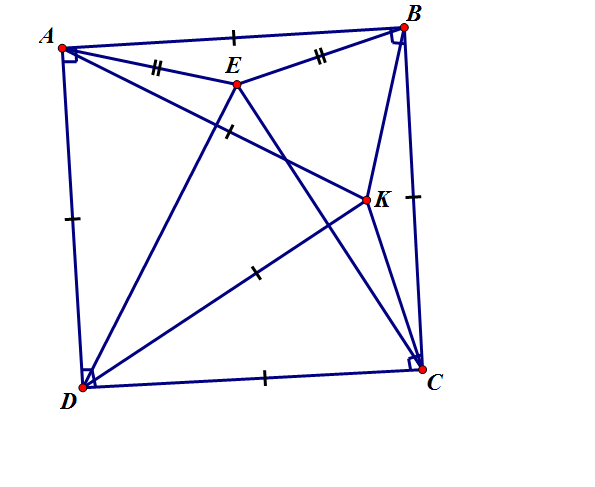
:-Lấy E' trong hình vuông ABCD sao cho tam giác DCE' đều.
-Ta có: DE'=DA và góc ADE'= 30 độ.
=> góc DAE'= 75 độ. Và có góc DAB=90 độ.
=> góc BAE'= 15 độ.
-Chứng minh tương tự, ta có góc ABE'=15 độ.
Suy ra điểm E trùng với E'.
Vậy tam giác DEC đều.
NHỚ TK MK NHA,
LT
3 tháng 2 2015
Có hai cách vẽ thêm hình phụ ở bài này:
Dựng tam giác đều IFB, I nằm trong tam giác CFB.
Hoặc ở phía ngoài hình vuông ABCD dựng tam giác ABH đều.
BT
2 tháng 11 2017
Phía trong của hình vuông ABCD ta dựng tam giác đều ADK. Ta có AD = AK = DK.
\(\widehat{DAK}=90^o-\widehat{KAD}=30^o\).
Do AB = AK (cùng bằng AD) nên tam giác BAK cân tại A.
Suy ra \(\widehat{ABK}=\widehat{AKB}=\frac{180^o-\widehat{BAK}}{2}=75^o\).
Suy ra \(\widehat{BKC}=90^o-\widehat{ABK}=15^o\).
Tương tự ta cũng có \(\widehat{KDC}=30^o,\widehat{DCK}=75^o,\widehat{KCB}=15^o\).
Dễ dàng chứng minh được \(\Delta ABE=\Delta BKC\left(g.c.g\right)\) nên AE = BE = BK = KC.
Từ đó ta chứng minh được \(\Delta AED=\Delta CDK\left(c.g.c\right)\).
Suy ra \(\widehat{ADE}=\widehat{KDC}=30^o\).
Suy ra tam giác CDE đều.