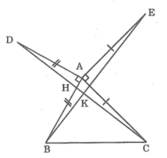
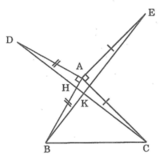
Cho tam giác ABC nhọn , vẽ AD vuông góc AB và AD=AB ( D và C khác phía với AB ) . vẽ AE vuông góc AC và AE=AC CE khác phía với B đối với AC . Chứng minh :\
a,DC=BE
b,DC⊥BE
c,Kẻ AH⊥BC(HϵBC);AH cắt DE tại M .Chứng minh M là trung điểm của DE
d,Gọi N là trung điểm của BC.Kẻ AN cắt DE tại F. Chứng minh AF⊥DE