Trong mặt phẳng (Oxy), cho \(d:x+y-2=0\)
Viết phương trình của đường thẳng d' là ảnh của d qua phép \(Q_{\left(0;45^0\right)}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ủa mà ID=d(I;(d)) mà sao ID2+d2(I;(d)) =3 vậy bạn
với lại R sao lại bằng ID+d(I;(d)) vậy bạn

Đáp án là B

x − 3 8 − 3 = y + 6 − 11 + 6 < = > − 5 x − 5 y − 15 = 0 < = > x + y + 3 = 0

Gọi M(x; y) tùy ý thuộc d, suy ra 3x – y + 2 = 0 (1)
Gọi M’(x’; y’) = ĐOy(M) ⇔ 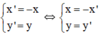
Thay vào (1), ta được : 3(-x’) – y’ + 2 = 0 ⇔ 3x’ + y’ – 2 = 0
Do đó, điểm M’ thuộc đường thẳng d’ : 3x + y – 2 = 0.
Vậy qua phép đối xứng trục Oy biến đường thẳng d thành đường thẳng d’: 3x + y- 2=0

Lấy A(2;6) thuộc d
Theo đề, ta có; \(\overrightarrow{IA'}=3\cdot\overrightarrow{IA}\)
=>\(\left\{{}\begin{matrix}x+7=3\left(2+7\right)\\y-2=3\left(6-2\right)\end{matrix}\right.\Leftrightarrow A'\left(20;14\right)\)
Thay x=20 và y=14 vào (d'): x-2y+c=0, ta đc:
c+20-28=0
=>c=8

Dễ thấy d chứa điểm H(1;1) và OH ⊥ d. Gọi H' là ảnh của H qua phép quay tâm O góc 45 o thì H ′ = ( 0 ; 2 ) . Từ đó suy ra d' phải qua H' và vuông góc với OH'. Vậy phương trình của d' là y = 2 .

Đáp án B.
Dễ thấy d ⊥ α và − 1 ; − 2 ; − 3 ∈ α ⇒ d ⊂ α .
Ta có B = Δ ∩ Oxy ⇒ B a ; b ; 0 mà B ∈ Δ ⊂ α ⇒ 2 a + b − 2 = 0 (1).
Lại có d / / Δ ⇒ d d ; Δ = d B ; d = 3.
Đường thẳng d đi qua M 0 ; 0 ; − 1 , có u d → = 1 ; 2 ; 2 .
Do đó:
d B ; d = B M → ; u d → u d → = 2 b − 2 2 + 1 − 2 a 2 + 2 a − b 2 3 = 3 2
Từ (1), (2) suy ra:
a ; b = − 1 ; 4 → B − 1 ; 4 ; 0 a ; b = 2 ; − 2 → B 2 ; − 2 ; 0 .
Vậy A B = 7 2 .