Từ nóc một cao ốc cao 30m, người ta nhìn thấy chân và đỉnh một cột ăng-ten với các góc hạ và nâng lần lượt là 450 và 600. Tính chiều cao của cột ăng-ten (kết quả làm tròn đến hàng đơn vị).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
trần trang
20 tháng 11 2018
Đúng(0)
Những câu hỏi liên quan
24 tháng 9 2023
Tham khảo:
a)
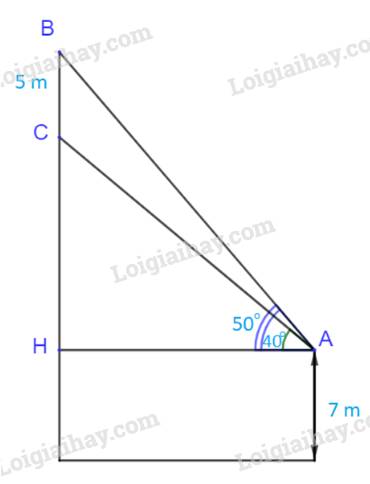
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)
\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)
Xét tam giác ABH, vuông tại H ta có:
\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)
\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)
Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)
Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).
b)
Áp dụng định lý sin cho tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)
Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)
\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)
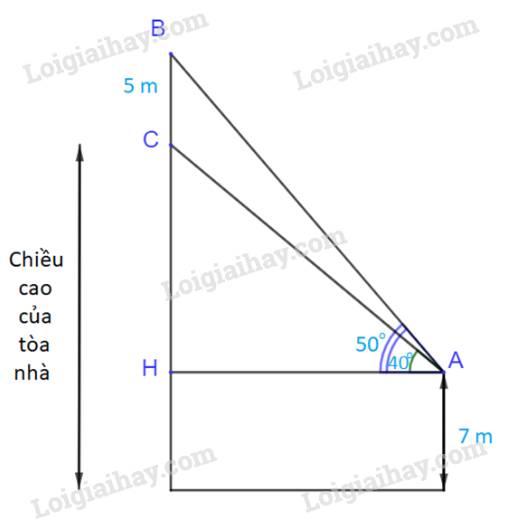
Xét tam giác ABH, vuông tại H ta có:
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)
Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)
\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)
Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)
1 tháng 3 2016
ve hinh thang vuong ABED co AD//BC ; va ED vuong goc voi BC keo dai ;
E thuoc BC keo dai(hinh chieu cua BC tren mat dat)
.D la diem duoi mat dat cua A AD=7m; BC=5m
Cac goc 40 ; 50 do la giua AC ; AB voi phuong nam ngang .
Ta tinh duoc DE theo BC : DE =BC/(tan50-tan40)
=> Bc da biet tan ta tra duoc .Con CE la chieu cao cua nha :
Vay : CE=AD+DE*tan40= 7+5*tan40/(tan50-tan40)